Ekuacioni i valës elektromagnetike
Ekuacioni i valës elektromagnetike është një ekuacion diferencial pjesor i rendit të dytë që përshkruan përhapjen e valës elektromagnetike përmes një mjedisi ose në boshllëk. Forma homogjene e ekuacionit, me terma të fushës elektrike E ose të fushës magnetike B, është i formës:
Ku c është shpejtësia e dritës në mjedisin e caktuar. Në vakuum shpejtësia e dritës është, c = c0 = 299,792,458 metër për sekondë.[1]
Ekuacioni i valës elektromagnetike derivohet nga ekuacionet e Maksuellit.
Duhet te theksohet se në literaturën e vjetër, B është "densiteti i fluksit magnetik" ose "induksioni magnetik".
Shpejtësia e përhapjes[Redakto | Redakto nëpërmjet kodit]
Në vakuum(boshllëk)[Redakto | Redakto nëpërmjet kodit]
Nëqoftëse vala përhapet në boshllëk, atëherë
- metër për sekonda,
është shpejtësia e dritës në vakum, një vlerë e përcaktuar që përcakton standardin e gjatësisë, njësisë së metrit. Konstantja magnetike dhe permitiviteti i vakumit janë dy konstante fizike të rëndësishme që luajnë një rol kryesor në teorinë elektromagnetike. Vlerat e tyre (të cilat janë gjithashtu të përcaktuar) në njësi SI të marra nga NIST janë tabuluar më poshtë :
| Simboli | Emri | Vlera Numerike | SI Njësia e matjes | Tipi |
|---|---|---|---|---|
| Shpejtësia e dritës nëe vakum | metër për sekondë | e përcaktuar | ||
| konstantja elektrike | Farad për metër | e derivuar; | ||
| konstantja magnetike | Henri për metër | e përcaktuar | ||
| Rezistenca karakteristike e vakumit | ohms | e derivuar; |
Në një mjedis material[Redakto | Redakto nëpërmjet kodit]
Shpejtësi e dritës në një mjedis material linear, isotropik, dhe jo-shperhapës ( jo-dispersiv) është
ku
është indeksi i refraktimit te mjedisit, është permiabiliteti magnetik i mjedisit, dhe është permitiviteti elektrik i mjedisit.
Origjina e ekuacionit të valës elektromagnetike[Redakto | Redakto nëpërmjet kodit]
Konservimi i ngarkesës elektrike[Redakto | Redakto nëpërmjet kodit]
Konservimi i ngarkesës kërkon që shpejtësia e ndryshimit në kohë te të gjithë ngarkesës elektrike të kufizuar brenda një volumi V duhet të jetë e barabarte korrentin total që rrjedh në sipërfaqen S e cila përmbyll volumin V :
ku j është densiteti i korrentit (në Amper për metër katror) që rrjedh përmes sipërfaqes dhe ρ është densiteti i korrentit (në kulomb për metër kub) në çdo pikë të volumit.
Nga teorema e divergjencës, ky relacion mund të konvertohet nga forma integrale në atë diferenciale :
Ligji i Amperit para korrektimit të Maksuellit[Redakto | Redakto nëpërmjet kodit]
Në formën e tij origjinale, Ligji i forcës së Amperit jep lidhjene midis fushës magnetike B dhe densitetit të korrentit j :
ku S është një sipërfaqe e hapur e kufizuar nga një kurbë C. Kjo forme integrale mund të shndërrohet në formën diferenciale me ane te teoremës së Stouks :
Mospërputhja midis ligjit të Amperit dhe ruajtjes së ngarkesës elektrike[Redakto | Redakto nëpërmjet kodit]
Po të marrim divergjencën e të dyja aneve të ligjit të forcës së Amperit kemi :
Divergjenca e rrotacionit të çdo fushë vektoriale, përfshire fushën magnetikë B, është gjithmonë zero :
Po të kombinojmë këto dy ekuacione del se
Për shkak se është një konstante jo-zero, rrjedh se
Megjithatë, ligji i ruajtjes së ngarkesës elektrike thotë se
Pra, si në rastin e ligjeve te Kircofit, ligji i forcës së Amperit është i vërtete vetëm në ato raste kur kemi të bëjmë me një situate që përfshin një densitet konstant ngarkese. Kjo nuk e përfshin situatën që ndosh kur kemi rikarikimin e pllakave te një kapacitete.
Korrektimi i Maksuellit dhe ligji rrethor i Amperit[Redakto | Redakto nëpërmjet kodit]
Ligji i Gausit në formën integrale pohon se :
ku S është një sipërfaqe e mbyllur që kufizon një volum V. Kjo formë integrale mund të konvertohet në formën diferenciale duke përdorur teoremën e divergjencës :
Po të marrim derivatin kohor te të dyja aneve dhe të nderojmë radhën e diferencimit në anën e majte marrim :
Ky rezultat i fundit së bashku me ligjin rrethor të Amperit (ligjin e forcës së Amperit) si dhe me ligjin e ruajtjes së ngarkesës elektrikë, sugjeron se aktualisht kemi dy burime origjine të fushës magnetikë : densiteti e korrentit j, siç e zbuloi Amperi, si dhe i ashtequajturi korrent zhvendoses:
Kështu që forma e rregullt e ligjit të forcës së Amperit bëhet :
Hipoteza e Maksuellit se drita është një valë elektromagnetike[Redakto | Redakto nëpërmjet kodit]

Në publikim e tij të 1864 të titulluar Nje teori Dinamike e fushës elektromagnetike, Maksuelli përdori korrigjimin e ligjit të forcës së Amperit të cilin ai kishte bëre në pjesën e III të publikimit të 1861-shit On Physical Lines of Force. Ne pjesene e VI të publikimit të 1864 të titulluar Teoria elektromagnetike e dritës[2], Maksuelli kombinoi korrentin zhvendoses me disa ekuacione të tjera të elektromagnetismit për të marre ekuacionin e valës elektromganetike me shpejtësi të barabarte me atë të dritës. Ai komentoi :
- Rënia dakord e rezultateve tregon se drita dhe magnetizmi janë ngacmime të të njejtes substance, si dhe drita është një valë elektromagnetike që përhapet përmes një fushë sipas ligjeve të elektromagnetizmit.[3]
Derivimi i Maksuellit për ekuacionin e fushës elektromagnetike është zëvendësuar në fizikën moderne nga një metode shumë më e thjështë që përfshin kombinimin e versionit të korrektuar të ligjit të forcës së Amperit me ligjin e induksionit të Faradeit.
Në mënyre që të marrim ekuacionin e valës elektromagnetike në boshllëk duke përdorur metodën moderne, mund të fillojmë me formën 'Hevisajd' të ekuacioneve të Maksuellit. Në vakum këto ekuacione janë :
Po të marrim rrotacionin e rrotacionit të ekuacioneve kemi :
Duke përdorur identitetin vektorial
ku është një funksion vektorial i hapësirës, marrim ekuacionin e valës :
ku
- metër për sekonda
është shpejtësia e dritës në boshllëk.
Forma kovariante e ekuacionit homogjen të valës[Redakto | Redakto nëpërmjet kodit]
Këto ekuacione relativiste mund të shkruhen në formë kovariante si
ku potenciali 4-dimensional elektromagnetik është
Me konditën e madhësisë së Lorencit :
- .
Këtu
- është simboli i operatorit d'Alembertian. Kutia katrore nuk është gabim tipografik ; ajo është simboli i këtij operatori.
Ekuacioni homogjen i valës në hapësire kohën e kurbuar[Redakto | Redakto nëpërmjet kodit]
- Artikulli kryesor: Ekuacionet e Maksuellit në hapësire-kohën e kurbuar
Ekuacioni i valës elektromagnetike modifikohet në dy mënyra, derivati zëvendësohet me derivation kovariant dhe një term i ri që varet në kurbaturën e hapësire-kohës shfaqet tek ekuacioni.
ku
ështe tensori i kurbaturës i Ricit dhe pikëpresja tregon diferencimin kovariant.
Përgjithësimi i konditës së madhësisë së Lorencit në hapësirën e kurbuar merret parasysh këtu :
- .
Ekuacioni johomogjen i valës elektromagnetike[Redakto | Redakto nëpërmjet kodit]
- Artikulli kryesor: Ekuacioni johomogjen i valës elektromagnetike
Ngarkesa lokale dhe densitete të korrentit që ndryshojnë në kohë veprojnë si burime të ngarkesës elektromagnetike në boshllëk. Ekuacionet e Maksuellit mund të shkruhen në formën e ekuacionit të valës me burime. Shtimi i burimeve tek ekuacioni i valës i bën ekuacionet diferenciale pjesore jo-homogjene.
Zgjidhje te ekuacionit homogjen të valës elektromagnetike[Redakto | Redakto nëpërmjet kodit]
- Artikulli kryesor: Ekuacioni i valës
Zgjidhja e përgjithshme e ekuacionit të valës elektromagnetike është një superpozim linear i valëve të formës
dhe
e cila virtualisht është e sakte për çdo funksion që sillet mirë g me një argument pa përmasa φ, ku
- është frekuenca këndore (në radian për sekonda), dhe
- është vektori i valës (në radiane për metër).
Edhe pse funksioni g mund të jetë dhe zakonisht është një vale sinusoidale monokromatike, ajo mund të mos jetë sinusoidale , ose periodike. Në praktikë, g nuk mund të ketë një periodicitet infinit sepse çdo vale elektromagnetike ka një zgjerim të kufizuar në hapësire dhe në kohë. Si rezultat i kësaj, dhe bazuar në teorinë e dekompozimit të Furierit, një valë reale konsiston si një mbivendosje e një bashkësie të pafundme frekuencash sinusoidale.
Për më tepër, për një zgjidhje të sakte, vektori i valës dhe frekuenca këndore nuk janë madhësi të pavarura ; këto madhësi aderojnë sipas relacionit dispersiv :
ku k është numri valor dhe λ është gjatësia e valës.
Gjendja monokromatike, sinusoidale[Redakto | Redakto nëpërmjet kodit]
Bashkësia më e thjështë e zgjidhjeve të ekuacionit të valës rezulton duke hipotezuar së forma sinusoidale e një frekuence të vetme në formë të ndarë :
ku
- është njësia imagjinare,
- është frekuenca këndore në radian për sekonda,
- është frekuenca në Herz, dhe
- është formula e Ojlerit.
Zgjidhjet e valës planare[Redakto | Redakto nëpërmjet kodit]
- Artikulli kryesor: Zgjidhjet sinusoidale planare të ekuacionit të valës elektromagnetike
Konsideroni një plan te përcaktuar nga një vektor njësi pingul
- .
Atëherë zgjidhjet e valës planare të ekuacionit të valës janë
dhe
ku
- është vektori i pozicionit (në metra).
Këto zgjidhje paraqesin një valë planare që udhëton në drejtimin e vektorit pingul . Po ta përcaktojmë drejtimin z si drejtimin e dhe drejtimin x si drejtimin e , atëherë nga ligji i Faradeit vijat e fushës magnetike shtrihen në drejtimin y dhe lidhen me fushën elektrike nga relacioni
- .
Për shaka se divergjenca e fushës elektrike dhe magnetike janë zero, nuk ka fusha në drejtimin e propagimit të valës.
Kjo zgjidhje ështe zgjidhja e polarizimit linear të ekuacionit të valës. Ekzistojnë edhe zgjidhje që janë të polarizuara në mënyre rrethore në të cilat fusha rrotullohet rreth vektorit normal.
Dekompozimi spektral[Redakto | Redakto nëpërmjet kodit]
Për shkak të linearitetit të ekuacioneve të Maksuellit në boshllëk, zgjidhjet mund të dekompozohen në një superpozim sinusoidesh. Kjo është ideja themelore e metodës së transformimit te Furierit për zgjidhjen e ekuacioneve diferenciale. Zgjidhja sinusoidale e ekuacionit të valës elektromagnetike merr formën
dhe
ku
- është koha (në sekonda),
- është frekuenca këndore (në radian për sekonda),
- është vektori i valës (në radiane për metër), dhe
- është kendi fazor (në radiane).
Vektori i valës është i lidhur me frekuencës këndore nga
ku k është numri valor dhe λ është gjatësia e valës.
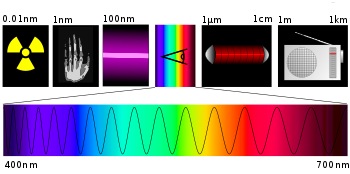
Spektri elektromagnetik është një graf i madhësive të fushës (ose energjisë) si funksion i gjatësisë së valës.
Zgjidhje te tjera[Redakto | Redakto nëpërmjet kodit]
Zgjidhje analitike sferikisht simetrike dhe cilindrikisht simetrike janë të mundura për ekuacionin e valës elektromagnetike. Në koordinata cilindrike ekuacioni i valës mund të shkruhet si më poshtë :
dhe
Shikoni gjithashtu[Redakto | Redakto nëpërmjet kodit]
Teoria dhe eksperimenti[Redakto | Redakto nëpërmjet kodit]
Aplikime[Redakto | Redakto nëpërmjet kodit]
Shenime[Redakto | Redakto nëpërmjet kodit]
- ^ Praktika e tanishme është që të përdorim c0 për të treguar shpejtësinë e dritës në vakum sipas ISO 31. Në rekomandimin origjinal të 1983, simboli c u përdor për këtë qëllim. Shiko NIST Special Publication 330, Appendix 2, p. 45 Arkivuar 3 qershor 2016 tek Wayback Machine
- ^ Maxwell 1864 4 (faqja 497 e artikullit si dhe faqja 9 e dokumentit pdf)
- ^ See Maxwell 1864 5, faqja 499 e artikullit dhe faqja 1 e linkut pdf
Referime[Redakto | Redakto nëpërmjet kodit]
Lexime të mëtejshme[Redakto | Redakto nëpërmjet kodit]
Elektromagnetizmi[Redakto | Redakto nëpërmjet kodit]
Artikuj gazetash[Redakto | Redakto nëpërmjet kodit]
- Maxwell, James Clerk, "A Dynamical Theory of the Electromagnetic Field", Philosophical Transactions of the Royal Society of London 155, 459-512 (1865). (This article accompanied a December 8, 1864 presentation by Maxwell to the Royal Society.)
Libra të nivelit universitar[Redakto | Redakto nëpërmjet kodit]
- Griffiths, David J. (1998). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 0-13-805326-X.
{{cite book}}: Mungon ose është bosh parametri|language=(Ndihmë!) - Tipler, Paul (2004). Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5th ed.). W. H. Freeman. ISBN 0-7167-0810-8.
{{cite book}}: Mungon ose është bosh parametri|language=(Ndihmë!) - Edward M. Purcell, Electricity and Magnetism (McGraw-Hill, New York, 1985). ISBN 0-07-004908-4.
- Hermann A. Haus and James R. Melcher, Electromagnetic Fields and Energy (Prentice-Hall, 1989) ISBN 0-13-249020-X.
- Banesh Hoffmann, Relativity and Its Roots (Freeman, New York, 1983). ISBN 0-7167-1478-7.
- David H. Staelin, Ann W. Morgenthaler, and Jin Au Kong, Electromagnetic Waves (Prentice-Hall, 1994) ISBN 0-13-225871-4.
- Charles F. Stevens, The Six Core Theories of Modern Physics, (MIT Press, 1995) ISBN 0-262-69188-4.
- Markus Zahn, Electromagnetic Field Theory: a problem solving approach, (John Wiley & Sons, 1979) ISBN 0-471-02198-9
Libra të nivelit post-universitar[Redakto | Redakto nëpërmjet kodit]
- Jackson, John D. (1998). Classical Electrodynamics (3rd ed.). Wiley. ISBN 0-471-30932-X.
{{cite book}}: Mungon ose është bosh parametri|language=(Ndihmë!) - Landau, L. D., The Classical Theory of Fields (Course of Theoretical Physics: Volume 2), (Butterworth-Heinemann: Oxford, 1987). ISBN 0-08-018176-7.
- Maxwell, James C. (1954). A Treatise on Electricity and Magnetism. Dover. ISBN 0-486-60637-6.
{{cite book}}: Mungon ose është bosh parametri|language=(Ndihmë!) - Charles W. Misner, Kip S. Thorne, John Archibald Wheeler, Gravitation, (1970) W.H. Freeman, New York; ISBN 0-7167-0344-0. (Provides a treatment of Maxwell's equations in terms of differential forms.)
Analiza vektoriale[Redakto | Redakto nëpërmjet kodit]
- P. C. Matthews Vector Calculus, Springer 1998, ISBN 3-540-76180-2
- H. M. Schey, Div Grad Curl and all that: An informal text on vector calculus, 4th edition (W. W. Norton & Company, 2005) ISBN 0-393-92516-1.








































































