Nga Wikipedia, enciklopedia e lirë
Brinjët dhe këndet e një trekëndëshi të çfarëdoshëm Teorema e kosinusit përdoret për gjetjen e brinjëve dhe këndeve të trekëndëshit të çfarëdoshëm. Ajo është përgjithësim i teoremës së famshme të Pitagorës e cila vlen për trekëndëshin këndrejt. Teorema njihet edhe me emrin "Teorema e Al-Kashit" dhe me fjalë ajo mund të formulohet si vijon:
Te çdo trekëndësh katrori i çdo brinje është i barabartë me shumën e katrorëve të dy brinjëve tjera i zvogëluar për dyfishin e prodhimit të tyre me kosinusin e këndit përballë asaj brinje.
a
2
=
b
2
+
c
2
−
2
b
c
cos
α
{\displaystyle a^{2}=b^{2}+c^{2}-2bc\cos \alpha }
b
2
=
a
2
+
c
2
−
2
a
c
cos
β
{\displaystyle b^{2}=a^{2}+c^{2}-2ac\cos \beta }
c
2
=
a
2
+
b
2
−
2
a
b
cos
γ
{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos \gamma }
Teorema është përgithësim i teoremës së Pitagorës e cila vlen nëse trekëndëshi ka një kënd të drejtë nëse supozojmë se p.sh. këndi γ është i drejtë 90°= π/2 radian atëherë cos(γ) = 0, prandaj
c
2
=
a
2
+
b
2
{\displaystyle c^{2}=a^{2}+b^{2}\,}
Ky barazim paraqet teoremën e Pitagorës.
Teorema përdoret për zgjidhjen e trekëndëshit
Në rast se janë dhënë tre brinjët e tij për gjetjen e këndeve
γ
=
cos
−
1
a
2
+
b
2
−
c
2
2
a
b
;
{\displaystyle \,\gamma =\cos ^{-1}{\frac {a^{2}+b^{2}-c^{2}}{2ab}}\,;}
Në rast se janë dhënë dy brinjë dhe këndi në mes tyre për gjetjen e brinjës së tretë dhe këndeve tjera
c
=
a
2
+
b
2
−
2
a
b
cos
(
γ
)
;
{\displaystyle \,c={\sqrt {a^{2}+b^{2}-2ab\cos(\gamma )}}\,;}
Në rast se janë dhënë dy brinjë dhe këndi përballë njërës prej tyre për gjetjen e brinjës së tretë dhe këndeve tjera
a
=
b
cos
(
γ
)
±
c
2
−
b
2
sin
2
(
γ
)
.
{\displaystyle \,a=b\cos(\gamma )\pm {\sqrt {c^{2}-b^{2}\sin ^{2}(\gamma )}}\,.}
Formulat nuk paraqiten teresisht ne kete forme
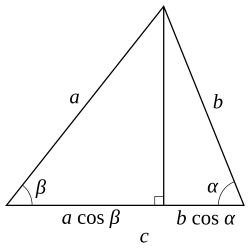
Lëshojmë lartësinë mbi brinjën c atëherë nga figura kemi
c
=
a
cos
(
β
)
+
b
cos
(
α
)
.
{\displaystyle c=a\cos(\beta )+b\cos(\alpha )\,.}
Nëse të njejtën gjë e përsërisim për lartësitë tjera atëherë kemi
b
=
c
cos
(
α
)
+
a
cos
(
γ
)
.
{\displaystyle b=c\cos(\alpha )+a\cos(\gamma )\,.}
c
=
a
cos
(
β
)
+
b
cos
(
α
)
.
{\displaystyle c=a\cos(\beta )+b\cos(\alpha )\,.}
Barazimin e parë e shumëzojmë me c të dytin me b dhe të tretin me a atëherë fitojmë
c
2
=
a
c
cos
(
β
)
+
b
c
cos
(
α
)
.
{\displaystyle c^{2}=ac\cos(\beta )+bc\cos(\alpha )\,.}
a
2
=
a
c
cos
(
β
)
+
a
b
cos
(
γ
)
,
{\displaystyle a^{2}=ac\cos(\beta )+ab\cos(\gamma )\,,}
b
2
=
b
c
cos
(
α
)
+
a
b
cos
(
γ
)
.
{\displaystyle b^{2}=bc\cos(\alpha )+ab\cos(\gamma )\,.}
I mbledhim dy barazimet e fundit atëherë kemi
a
2
+
b
2
=
a
c
cos
(
β
)
+
b
c
cos
(
α
)
+
2
a
b
cos
(
γ
)
{\displaystyle a^{2}+b^{2}=ac\cos(\beta )+bc\cos(\alpha )+2ab\cos(\gamma )\,}
Prej këtij barazimi e zbresim të parin atëherë fitojmë
a
2
+
b
2
−
c
2
=
−
a
c
cos
(
β
)
−
b
c
cos
(
α
)
+
a
c
cos
(
β
)
+
b
c
cos
(
α
)
+
2
a
b
cos
(
γ
)
{\displaystyle a^{2}+b^{2}-c^{2}=-ac\cos(\beta )-bc\cos(\alpha )+ac\cos(\beta )+bc\cos(\alpha )+2ab\cos(\gamma )\,}
nga barazimi i fundit pas thjeshtimeve të mundshme fitojmë se
c
2
=
a
2
+
b
2
−
2
a
b
cos
(
γ
)
.
{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos(\gamma ).\,}