Teorema e Talesit

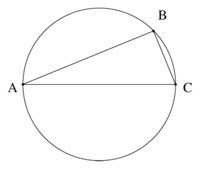
Teorema e Talesit thotë se: Nëse $\quad A,B$ dhe $\quad C$ janë pika të një vije rrethore të tilla që segmenti $\quad AC$ është diametër i vijës rrethore atëherë këndi $\quad ABC$ është kënd i drejtë.

Vërtetimi

Kemi parasysh se shuma e këndeve të trekëndëshit është sa dy kënde të drejta dhe këndet te baza e një trekëndëshi barakrahës janë të barabarta.

Le të jetë $\quad O$ qendra e trekëndëshit. Pasi $\quad OA=OB=OC$ , përfundojmë se trekëndëshat $\quad OAB$ dhe $\quad OBC$ janë trekëndësha barakrahës prandaj $\quad OBC=OCB$ dhe $\quad BAO=ABO$ . Shënojmë $\quad \gamma =BAO$ dhe $\quad \delta =OBC$ .

Pasi shuma e këndeve të trekëndëshit është 180° kemi se:

$\quad 2\gamma +\gamma '=180^{\circ }$

dhe

$\quad 2\delta +\delta '=180^{\circ }$

e dijmë se

$\quad \gamma '+\delta '=180^{\circ }$

Duke i mbledhur dy barazimet e para prej të cilës shumë e zbresim barazimin e tretë fitojmë

$\quad 2\gamma +\gamma '+\quad 2\delta +\delta '-(\gamma '+\delta ')=180^{\circ }$

pas anulimit të $\quad \gamma '$ dhe $\quad \delta '$ , fitojmë se

$\quad \gamma +\delta =90^{\circ }$

Teorema e anasjelltë e Talesit

Teorema e anasjelltë e Talesit thotë se: Hipotenuza e trekëndëshit kënddrejt është diametër i rrethit të jashtashkruar.

Nëse e kombinojmë teoremën e Talesit me të anasjelltën e saj atëherë kemi teoremën vijuese: Qendra e rrethit të jashtashkruar të trkëndëshit shtrihet në njërën prej brinjëve të trkëndëshit atëherë dhe vetëm atëherë nëse trekëndëshi është kënddrejt.

Vërtetimi i teoremës së anasjelltë

Vërtetimi konsiston në atë që trekëndëshi këndrejt të plotësohet deri katërkëndësh këndrejt duke vërejtur se qendra e tij është njësoj e larguar nga kulmet e tij dhe është njëkohësisht qenddër e rretit të jashtashkruar. Kemi parasysh këto fakte:

Këndet e kundërta të paralelogramit janë suplementar pra shuma e tyre është 180° dhe,
diagonalet e kënddrejtit janë të barabarta dhe priten në mesin e tyre.

Le të jetë ABC një kënd i drejtë, r një drejtëzë paralele me BC e cila kalon nëpër A dhe s një drejtëzë paralele me AB që kalon nëpër pikën C. Le të jetë D pika ku priten drejtëzat r dhe s (Vërejmë se ne ende nuk kemi vërtetuar se pika D i takon rrethit)

Katërkëndëshi ABCD sipas mënyrës si e konstruktuam është paralelogram. Pra këndet e kundërta japin shumën 180° dhe këndi ABC është i drejtë (90°) atëherë këndet BAD, BCD, dhe ADC janë të drejta (90°); rrjedhimisht katërkëndëshi ABCD është kënddrejt.

Le të jetë O pikëprerja e diagonaleve AC dhe BD. Atëherë pika O, sipas fakteve që përmendëm më sipër është njësoj e larguar nga pikat A,B, dhe C. Pra ajo është qendër e rrethit të jashtashkruar dhe hipotenuza AC është diametër i tij.

Zbatimi i teoremës së Talesit

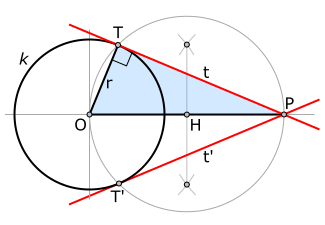
Teorema e Talesit përdoret për konstruktimin e tangjentës së rrethit nga një pikë e dhënë Le të jetë dhënë rrethi k, me qendër në pikën O, dhe pika P jashtë rrethit, të konstruktohet tangjenta (s) e rrethit k(në të kuqe) e cila kalon nëpër pikën P. Supozojmë se tangjenta që e kërkojmë t e prek rrethin në pikën T. Nga simetria është e qartë se rrezja OT është normale me tangjentën. Pra duhet të caktjmë pikën e mesit të segmentitHO dhe pikën P, pastaj konstruktojmë një rreth me qendër në H në mes O dhe P. Sipas teoremës së Talesit pika e njohur T është prerja e këtij rrethi me rrethin e dhënë k, pasi ajo është pika në rrethin k e cila formon trekëndëshin kënddrejt OTP.

Pasi dy rrathët priten në dy pika të ndryshme kjo do të thotë se nga një pikë jashtë rrethit të dhënë mund të tërhiqen dy tangjenta të rrethit. kjo ishte per rrethin nga une kaq dija

Historia

Tales nuk është i pari që e zbuloi teoremën, dihet se këtë teoremë e zotëronin Egjiptianët dhe Babilonasit e lashtë të cilët e përdornin por pa e vërtetuar. Talesi është i pari që dha vërtetimin e saj prandaj ajo sot mban emrin e tij.

Lidhje të jashtme

Munching on Inscribed Angles
Thales' theorem explained Me animacione interaktive
Thales' Theorem by Michael Schreiber, The Wolfram Demonstrations Project.
Eric W. Weisstein, Teorema e Talesit nga MathWorld.