Rrethi
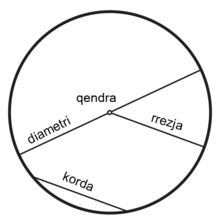
Rrethi është një vijë e lakuar e mbyllur ku çdo pikë e kësaj vije ka largesë të barabartë nga një pikë që quhet qendra e rrethit. Largesa ndërmjet një pike në rreth me qendrën e tij quhet rreze, ndërsa segmenti që bashkon dy pika të një rrethi dhe që kalon nëpër qendër quhet diametër. Korda është segmenti që bashkon dy pika çfarëdo të një rrethi; korda më e gjatë është diametri.
Ekziston një dallim mes rrethit dhe qarkut. Qarku nënkupton rrethin së bashku me sipërfaqen e brëndshme të tij.
Perimetri
[Redakto | Redakto nëpërmjet kodit]Nga përllogaritjet, raporti i perimetrit të rrethit ndaj diametrit është një konstante , një numër irracional përafërsisht i barabartë me 3.141592654. Kështu perimetri lidhet me rrezen sipas formulës:
ku është një numër i pafundëm joperiodik. Me marrëveshje, merret 3.14, ose lihet si konstante .
Sipërfaqja e rrethit
[Redakto | Redakto nëpërmjet kodit]
Sipërfaqja e rrethit gjendet duke shumëzuar pi-në me katrorin e rrezes:
- .
Ekuacionet e rrethit
[Redakto | Redakto nëpërmjet kodit]Në koordinata karteziane, pra ato të cilat lexuesi është mësuar, rrethi me qëndër në koordinatat (a,b) dhe rreze r është bashkësia e të gjithë pikave (x,y) të tilla që:
Derivimi i ekuacionit në koordinata karteziane
[Redakto | Redakto nëpërmjet kodit]Derivimi i këtij ekuacioni është i lehtë. Largesa mes dy pikave dhe në koordinatat karteziane jepet me anë të formulës:
Nga vetitë e rrethit, ne duam që kjo largësi nga qendra të jetë e barabartë me për çdo pikë të planit koordinativ. Duke shënuar qëndrën si dhe një pikë të çfarëdoshme si , i zëvëndësojmë këto të dhëna në relacionin e mësipërm:
Më pas ngremë në katror të dyja anët e ekuacionit për të mbërritur në atë çfarë deshëm të vërtetojmë:
Vetitë e rrethit
[Redakto | Redakto nëpërmjet kodit]- Nëse dy korda të një rrethi janë të barabarta, atëherë ato janë njësoj të baraslarguara nga qendra e rrethit dhe anasjelltas.
- Dy korda të barabarta të një rrethi tendosin harqe të barabarta dhe anasjelltas.
- Diametri pingul me kordën e ndan kordën dhe harkun që ajo tendos në dy pjesë të barabarta.
- Kur drejtëza (d) e prek rrethin nga jashtë vetëm në një pikë (është tangjente) me rrethin atëherë rrezja e rrethit është pingule me këtë drejtëz.
- Këndi qendror është këndi që ka si kulm qendrën e rrethit dhe brinjët e tij janë rreze të rrethit. Masa e harkut që formon ky kënd është e barabartë me masën e këtij këndi.
- Këndi rrethor është këndi që e ka kulmin në një pikë të rrethit dhe brinjët e tij janë korda të rrethit. Masa e harkut që tendos ky kënd është sa dyfishi i masës së këtij këndi.











