Vlera absolute
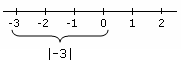
Në matematikë vlera absolute ose moduli |x| i një numri real x është vlera jo-negative e x pa marrë në konsideratë shenjën e tij. Si rrjedhim për numrat pozitive, më të mëdhenj se zero, |x| = x, ndërsa për numrat negative |x| = -x, dhe për numrin zero |0| = 0. Në boshtin numerik vlera absolute e një numri mund të konsiderohet si largësia e tij nga zeroja.
Përgjithësime të vlerës absolute të numrave reale mund të bëhen dhe për bashkësi të tjera numrash si psh për numrat komplekse, hapësirat vektoriale, fushat etj. Koncepti i Vlerës Absolute është i lidhur me konceptet e magnitudës, distancës, normës.
Terminologji[Redakto | Redakto nëpërmjet kodit]
Jean-Robert Argand përdori për herë të parë termin "module", dmth 'njësi matëse' në Frëngjisht, në vitin 1806 për vlerën absolute të numrave kompleks [1][2]. Më pas në 1866 ky term u huazua në Anglisht si ekuivalenti Latin i fjalës "modulus".[1] Termi "modul" në frëngjisht u përdor në këtë kuptim nga viti 1806 [3] dhe në anglisht "absolute value" nga viti 1857 [4] .
Shënimi matematikor ose simboli me dy vija vertikale |X| u përdor për herë të parë nga Karl Weierstrass in 1841.[5]. Emërtime të tjera për vlerën absolute janë "vlera numerike" [1] dhe "magnituda".[1]
I njëjti simbol është përdorur në bashkësitë për të treguar kardinalitetin e bashkësisë. Kuptimi i simbolit varet nga konteksi i përdorimit.
Përkufizimi dhe vetitë[Redakto | Redakto nëpërmjet kodit]
Numrat Reale[Redakto | Redakto nëpërmjet kodit]
Përkufizimi[Redakto | Redakto nëpërmjet kodit]
Për cdo numër real x vlera absolute e tij shënohet me |x| dhe përkufizohet si: .
Vlera absolute e një numri real x është gjithmonë një numër pozitiv ose 0, por asnjëherë numër negativ.
Vëmë re që .
Vetitë[Redakto | Redakto nëpërmjet kodit]
Për cdo numër real a dhe b vlera absolute gëzon vetitë e mëposhtme:
- (mosbarazim trekëndorsh)
- (mosbarazim trekëndorsh)
- (mosbarazim trekëndorsh i përgjithësuar për një familje numrash )
- (ku b një numër real pozitiv, nëse b është negativ nuk ka zgjidhje)
- (nëse b është negativ, atëherë zgjidhje jane të gjithë numrat real)
- ^ a b c d Oxford English Dictionary, Draft Revision, June 2008
- ^ Nahin, O'Connor and Robertson, dhe functions.Wolfram.com.; dhe në Frëngjisht lexo Dictionnaire de la langue française (Littré), 1877
- ^ Lazare Nicolas M. Carnot, Mémoire sur la relation qui existe entre les distances respectives de cinq point quelconques pris dans l'espace, p. 105 at Google Books
- ^ James Mill Peirce, A Text-book of Analytic Geometry at Google Books. Citimi më i vjeter në Botimin e dytë të Oxford English Dictionary është në 1907. Termi "vlerë absolute" përdoret gjithashtu në kontrast me "vlerën relative".
- ^ Nicholas J. Higham, Handbook of writing for the mathematical sciences.













