Qarku (matematikë)

Qarku me - perimetër C- diametër D - rreze R- qëndër O

Në gjeometri, një qark është rajoni në një plan të kufizuar nga një rreth . Një qark quhet i mbyllur nëse përmban rrethin që përbën kufirin e tij dhe i hapur nëse nuk e përmban.

Për një rreze, $r$, një qark i hapur zakonisht shënohet si $D_{r}$ dhe një qark i mbyllur është ${\overline {D_{r}}}$ . Megjithatë në fushën e topologjisë qarku i mbyllur zakonisht shënohet si $D^{2}$ ndërsa qarku i hapur është $\operatorname {Int} D^{2}$ .

Formulat

Në koordinatat karteziane, qarku i hapur i qendrës $(a,b)$ dhe rrezja R jepet me formulën:

$D=\{(x,y)\in {\mathbb {R} ^{2}}:(x-a)^{2}+(y-b)^{2}<R^{2}\}$

ndërsa qarku i mbyllur i së njëjtës qendër dhe rreze jepet nga:

${\overline {D}}=\{(x,y)\in {\mathbb {R} ^{2}}:(x-a)^{2}+(y-b)^{2}\leq R^{2}\}.$

Sipërfaqja e një qarku të mbyllur ose të hapur me rreze R është $\pi R^{2}$ .

Si shpërndarje statistikore

Largësia mesatare në një vend nga pikat në një qark

Një shpërndarje uniforme në një qark rrethor njësi haset herë pas here në statistikë. Më së shpeshti ndodh në kërkimet operacionale në matematikën e planifikimit urban, ku mund të përdoret për të modeluar një popullsi brenda një qyteti. Përdorime të tjera mund të përdorin faktin se është një shpërndarje për të cilën është e lehtë të llogaritet probabiliteti që një grup i caktuar inekuacionesh lineare do të plotësohet.

Nëse na jepet një vendndodhje arbitrare në një distancë $q$ nga qendra e diskut, është gjithashtu me interes të përcaktojmë largësinë mesatare $b(q)$ nga pikat në shpërndarje në këtë vendndodhje dhe katrorin mesatar të largësive të tilla. Vlera e fundit mund të llogaritet drejtpërdrejt si $q^{2}+{\frac {1}{2}}$

Distanca mesatare në një pikë të brendshme arbitrare

Largësia mesatare nga një qark në një pikë të brendshme

Për të gjetur $b(q)$ duhet të shikojmë veçmas rastet në të cilat vendndodhja është e brendshme ose e jashtme, dmth në të cilat q ≶ 1, dhe gjejmë se në të dyja rastet rezultati mund të shprehet vetëm në terma të integraleve të plota eliptike .

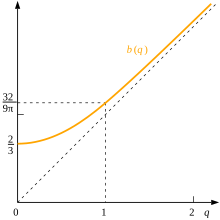
Nëse marrim parasysh një vendndodhje të brendshme, qëllimi ynë (duke parë diagramin) është të llogarisim vlerën e pritur të $r$ nën një shpërndarje, dendësia e së cilës është ${\frac {1}{\pi }}$ për $0\leq r\leq s(\theta )$, duke integruar në koordinata polare në vendndodhjen fikse për të cilën sipërfaqja e qelizës është $rdrd\theta$ kështu

$$b(q)={\frac {1}{\pi }}\int _{0}^{2\pi }{\textrm {d}}\theta \int _{0}^{s(\theta )}r^{2}{\textrm {d}}r={\frac {1}{3\pi }}\int _{0}^{2\pi }s(\theta )^{3}{\textrm {d}}\theta .$$

Këtu $s(\theta )$ mund të gjendet në termat e q dhe θ duke përdorur Ligjin e kosinuseve . Hapat e nevojshëm për të vlerësuar integralin, së bashku me disa referenca, do të gjenden në punimin e Lew et al.; rezultati është se

$$b(q)={\frac {4}{9\pi }}{\biggl \{}4(q^{2}-1)K(q^{2})+(q^{2}+7)E(q^{2}){\biggr \}}$$

ku K dhe E janë integrale të plota eliptike të llojit të parë dhe të dytë. $b(0)={\frac {2}{3}}$ ; $b(1)={\frac {32}{9\pi }}\approx 1.13177$

Largësia mesatare tek një pikë e jashtme arbitrare

Largesa mesatare nga një disk në një pikë të jashtme

Duke u kthyer në një vendndodhje të jashtme, ne mund të vendosim integralin në një mënyrë të ngjashme, këtë herë duke marrë

$$b(q)={\frac {2}{3\pi }}\int _{0}^{{\textrm {sin}}^{-1}{\tfrac {1}{q}}}{\biggl \{}s_{+}(\theta )^{3}-s_{-}(\theta )^{3}{\biggr \}}{\textrm {d}}\theta$$

ku ligji i kosinusit na tregon se $s_{+}(\theta )$ dhe $s_{-}(\theta )$ janë rrënjët për s tek ekuacioni:

$$s^{2}-2qs\,{\textrm {cos}}\theta +q^{2}\!-\!1=0.$$

Prandaj

$$b(q)={\frac {4}{3\pi }}\int _{0}^{{\textrm {sin}}^{-1}{\tfrac {1}{q}}}{\biggl \{}3q^{2}{\textrm {cos}}^{2}\theta {\sqrt {1-q^{2}{\textrm {sin}}^{2}\theta }}+{\Bigl (}1-q^{2}{\textrm {sin}}^{2}\theta {\Bigr )}^{\tfrac {3}{2}}{\biggl \}}{\textrm {d}}\theta .$$

Mund të zëvendësojmë $u=q\sin \theta$ për të marrë

$${\begin{aligned}b(q)&={\frac {4}{3\pi }}\int _{0}^{1}{\biggl \{}3{\sqrt {q^{2}-u^{2}}}{\sqrt {1-u^{2}}}+{\frac {(1-u^{2})^{\tfrac {3}{2}}}{\sqrt {q^{2}-u^{2}}}}{\biggr \}}{\textrm {d}}u\\[0.6ex]&={\frac {4}{3\pi }}\int _{0}^{1}{\biggl \{}4{\sqrt {q^{2}-u^{2}}}{\sqrt {1-u^{2}}}-{\frac {q^{2}-1}{q}}{\frac {\sqrt {1-u^{2}}}{\sqrt {q^{2}-u^{2}}}}{\biggr \}}{\textrm {d}}u\\[0.6ex]&={\frac {4}{3\pi }}{\biggl \{}{\frac {4q}{3}}{\biggl (}(q^{2}+1)E({\tfrac {1}{q^{2}}})-(q^{2}-1)K({\tfrac {1}{q^{2}}}){\biggr )}-(q^{2}-1){\biggl (}qE({\tfrac {1}{q^{2}}})-{\frac {q^{2}-1}{q}}K({\tfrac {1}{q^{2}}}){\biggr )}{\biggr \}}\\[0.6ex]&={\frac {4}{9\pi }}{\biggl \{}q(q^{2}+7)E({\tfrac {1}{q^{2}}})-{\frac {q^{2}-1}{q}}(q^{2}+3)K({\tfrac {1}{q^{2}}}){\biggr \}}\end{aligned}}$$

duke përdorur integrale standarde.

Prandaj përsëri $b(1)={\frac {32}{9\pi }}$

$$\lim _{q\to \infty }b(q)=q+{\tfrac {1}{8q}}.$$