Integrali

Në matematikë, integrali është analogu i vazhdueshëm i shumës i cili përdoret për të llogaritur sipërfaqet, vëllimet dhe përgjithësimet e tyre. Integrimi, procesi i llogaritjes të integralit, është një nga dy veprimet thelbësore të njehsimit diferencial dhe integral ndërsa tjetri është diferencimi. Integrimi filloi si një metodë për të zgjidhur problemat në matematikë dhe fizikë, siç janë gjetja e sipërfaqjes poshtë një grafiku ose përcaktimi i zhvendosjes nga shpejtësia. Sot integrimi përdoret në një shumëllojshmëri të fushave të shkencës.

Integralet e renditura këtu quhen integrale të caktuara, të cilët mund të interpretohen si zona e shënuar në një vend të planit e cila është e kufizuar nga një grafik i një funksioni të dhënë ndërmjet dy pikave në boshtin e numrave real. Për lehtësi, zonat sipër boshtit të abshisave janë pozitive ndërsa ato poshtë janë negative. Integralet gjithashtu i referohen konceptit të integralit të pacaktuar. Teorema themelore e njehsimit diferencial dhe integral lidh integralet e caktuara me diferencimin dhe ofron një metodë për të llogaritur integralin e caktuar të një funksioni nëse dihet antiderivati i tij. Diferencimi dhe integrimi janë veprime të kundërta.

Edhe pse metoda për llogaritjen e sipërfaqeve dhe vëllimeve daton që nga matematika e grekëve të lashtë, parimet e integrimit u formuluan në mënyrë të pavarur nga Isak Njutoni dhe Gotfrid Vilhelm Lajbnici në fundin e shekullit të 17-të, të cilët e menduan sipërfaqen poshtë një grafiku si shuma e pafundme e drejtkëndëshave me gjerësi pambarimisht të vogël. Më vonë Bernard Riman dha një përcaktim rigoroz të integraleve i cili bazohej në një procedurë kufizuese e cila përafron sipërfaqen e një zone të lakuar duke e ndarë zonën në pllaka pambarimisht të holla. Në fillim të shekullit të 20-të Enri Lëbeg përgjithësoi formulimin e Rimanit duke shtuar atë që sot njihet si integrali i Lëbegut. Ky i fundit është më i fuqishëm se ai i Rimanit në kuptimin që një kategori më e madhe e funksioneve janë të integrueshme.

Integralet mund të përgjithësohen në varësi të llojit të funksionit dhe hapsirës në të cilën bëhet integrimi. Për shembull, një integral i një vije përcaktohet për funksione me dy ose më shumë ndryshore dhe intervali i integrimit zëvendësohet nga një lakore e cila lidh dy skajet e intervalit. Në një integral të sipërfaqes lakorja zëvendësohet nga një pjesë e sipërfaqes në hapësirën tre dimensionale.

Historia

Artikulli kryesor: Analiza matematike

Forma integrale janë përdorur që në kohën e Egjyptit të vjetër rreth 1800 vite p.e.s., për të cilat gjënden dokumente në materialin e njohur si Papirusi Matematik Mokovit, ku janë të demonstruara njohuri mbi formulën përmes së cilës është llogaritur vëllimi i frustumit piramidal. Dokumentimi i parë i teknikës sistematike të aftë për vendosjen e integralëve është metoda exhaustion e Eudoksusit (rreth vitit 370 p.e.s.), e cila provon të llogarisë hapësirat dhe vëllimet duke i ndarë ato në numëra të pa caktuar të formave për të cilët hapësira apo vëllimi njihen. Kjo metodë u zhvillua më mbas dhe u aplikua nga Arkimedi dhe u përdor për llogaritjen e hapësirave të parabolave dhe për përafrim të hapsirës së rrethit. Metoda të ngjashme të pa varura nga njëra tjetra u zhvilluan edhe në Kinë rreth shekullit III nga Liu Hui, i cili i përdori ato për të gjetur hapësirën e rrethit. Kjo metodë më vonë u përdor nga Zu Chongzhi për të gjetur vëllimin e sferës.

Ndryshime të dukshme të këtyre metodave nuk u vërjtën deri në shekullin XVI kur u paraqit Bonaventura Cavalieri me metodën e tijë të pandashmërisë dhe Fermat i cili filloi t'i vendosë themelet e analizës matematike. Hapat e mëtejëm u bënë në fillim të shekullit XVII nga Isaac Barrow dhe Evangelista Torricelli, të cilët përgatitën aludimet e para të lidheve në mes integrimit dhe diferencimit.

Newton dhe Leibniz (Njutën dhe Lajbnic)

Përparim i madh në metodat e integrimit u bë në shekullin e XVII me zbulimin e teoremës themelore të analizës matematike nga Isaac Newton dhe Leibniz, të cilët zhvilluan të pavarur nga njëri tjetri. Teorema demostron një lidhje të integrimit dhe diferencimit. Kjo lidhje e kombinuar me lehtësinë krahasuese të diferencimit mund të përdoret për llogaritjen e integraleve. Pjesërisht teorema themelore e analizës matematike mundëson zgjedhjen e problemeve shumë më të mëdhenjë. Rëndësi të njëjtë ka dhe struktura e kuptueshme matematikore të cilën e zhvilluan po ashtu Newton dhe Leibniz.

Hyrje

Integralet paraqiten në shumë situata praktike. Le të marrim shembull një pishinë. Duke marrë parasyshë gjatësinë, gjerësinë dhe thellësinë e pishinës me shumë lehtësi mund të llogarisim vëllimin e ujit (i cili duhet për të mbushur pishinën), gjithashtu mund të llogarisim syprinën (për të mbuluar) dhe gjatësinë e këndeve (për ta rrethuar). Nëse është i rrumbullakët me fund formë rrethi për të llogaritur tëgjitha këto të dhëna duhet përdorur integralet. Llogaritja e përafërt në jetën praktike mund të na kryen punë por jo edhe nëse na nevojiten rezultate të sakta dhe precize.

Përafrimi i integralit të √x nga 0 deri në 1, me ■ 5 shëmbujt djathtas (sipër) dhe ■ 12 shëmbujt majtas (poshtë)

Le të marrim lakoren y = f(x) mes x = 0 dhe x = 1, me f(x) = √x.

Duam të gjejmë: Sa është sipërfaqa nën funksionin f,në intervalin nga 0 në 1?

Pra tani e dimë se ky quhet integrali i f-së dhe formula do të jetë:

$\int _{0}^{1}{\sqrt {x}}\,dx\,\!$.

Shih njësinë e dhënë nga x=0 në x=1 dhe y=f(0)=0 dhe y=f(1)=1 që nënkupton se hapësira është 1. Sikur që shihet, vlera e vërtetë e integralit duhet të jetë më e vogël se 1. Duke zvogëluar gjerësinë e drejtkëndëshit të përafërt duhet të na japë rezultat më të mirë, pra letë kalojmë intervalin në pesë hapa duke përorur pikën 0, ¹⁄₅, ²⁄₅ duke vazhduar kështu gjer tek numri 1. Përshtatë kutinë për secilin hap duke shfrytëzuar anën e djathtë dhe lartësinë e çdo pjese të lakores, kështu √¹⁄₅, √²⁄₅ duke vazhduar kështu gjer tek √1 = 1. Due mbledur hapësirat e këtyre këndrejtëve gjejmë përafërsi më të saktë për integralin e kërkuar, kryesisht:

√¹⁄₅*( ¹⁄₅-0)+√²⁄₅*( ²⁄₅-¹⁄₅)+...+√⁵⁄₅*( ⁵⁄₅-⁴⁄₅) ≈ 0.7497.

Vërejmë se ne jemi duke marrë shumën e numrit të caktuar të shumë vlerave të funksionit f, të shumëzuara me ndryshimt e dy pikave të përafërta pasuse (që pasojnë njëra tjetrë). Mundemi lehtë të shohim përafërsia akoma është e madhe, por nëse përdorim më shumë hapa dë të zvogëlojmë përafërsinë megjithatë asnjëherë nuk munë të jemi të përpiktë. Duke zëvendësuar 5 nënintervalet me 12 ne do të fitojmë një vlerë të përafërt për hapësirën që është 0.6203, që është shumë e vogël. Qëllimi kryesorë është futja e shumë pikave (numër të caktuar pikash) të përafërta të shumëzuara me vlerat e funksoneve të tyre duke përdorur hapa të caktuar. Paraqitja në funksion:

$\int f(x)\,dx\,\!$

Nën kushte të përshtatshme vlera e një integrali mbi një hapësirë mund të caktohet duke shikuar në kufijtë e hapësirës. Aplikuar në rrëmnjën katroe të lakores duhet shikuar tek funksioni i përbashkët F(x) = ²⁄₃√x³, dhe duhet marrë F(1)−F(0), ku 0 dhe 1 janë kufijtë e intervalit [0,1]. (Ky është një shembull i rregullës së përgjithëshme ku për f(x) = x^q, me q ≠ −1, funksioni i ngjashëm i njohursi kundërderivat është F(x) = (x^q+1)/(q+1).)

Përkufizimi formal

Ka shumë rrugë të përkufizimit formal të një integrali, por nuk janë të gjitha ekuivalente. Dallimet paraqiten më së shumti gjatë problemeve me raste të pa integrueshme me nën përkufizime tjera, por gjithashtu rastësisht për arsye pedagogjike. Përkufizimet i cili përdoret më së shpeshti për integralet janë integralet e Riemann dhe integralet e Lebesgue.

Integrali i Riemann-it

Integrali i Riemann-it. (max në të kuqe). Vlera e vërtetë është 3.76; vlera e arritur 3.648.

Integrali i Riemann-it (i Bernhard Riemann) është përcaktuar nën kushtet e shumës së funksioneve sipas Riemann-it duke respektuar ndarjet e etiketuara të një intervali. Le të jetë [a,b] një interval i mbyllur i një vije , ku ndarja e etiketuar e [a,b] është sekuensë e numërueshme:

$a=x_{0}\leq t_{1}\leq x_{1}\leq t_{2}\leq x_{2}\leq \cdots \leq x_{n-1}\leq t_{n}\leq x_{n}=b.\,\!$

Shumat e Riemann-it duke u konvertuar ashtu si përgjysmohet intervali, qoftë tek shembulli ■ djathtas, ■ minimum, ■ maksimum, apo ■ majtas.

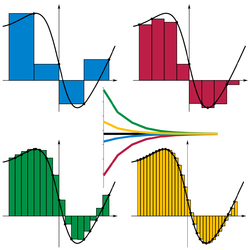
Kjo e ndanë intevalin [a,b] në i nën intervale[x_i−1, x_i], k secili është i "etiketuar" me pikë të caktuar t_i ∈ [x_i−1, x_i]. Le të jetë Δ_i = x_i−x_i−1 gjerësia e nen-intervalit i; pastaj rrjeta e ndarjeve të tilla të etiketuara është gjerësia e nën-intervalit më të madhë të krijuar nga ndarjet, max_i=1…n Δ_i. Shuma e Riemann-it e funksionit f me respekt ndaj pjesëve të tilla të etiketuara definohet si:

$\sum _{i=1}^{n}f(t_{i})\Delta _{i};$

kështu çdo shprehjes e shumës është hapësirë e drejtkëndëshit me lartësi të barabatë me vlerën e funksionit në pikën e caktuar të nën-intervalit të dhënë dhe gjerësia e njejtë me gjerësinë e nën-intervalit. Integrali i Riemann-it i funksionit f mbi intervalin [a,b] është i barabartë me S nëse:

Për të gjitha ε > 0 ekziston δ > 0 ku për çdo pjesë të etiketuar [a,b] me më pakë rrjetë se δ, kemi:

$\left|S-\sum _{i=1}^{n}f(t_{i})\Delta _{i}\right|<\epsilon .$

Kur etiketat e mbyllura japin vlerën maksimale (respektivisht minimale) të çdo intervali, atëherë shuma e Riemann-it më e lartë (respektivisht e ulët) se shuma e Darboux-it, duke sugjeruar lidhjen e afërt mes integralit të Riemann-it dhe integralit të Darboux-it.

Integrali i Lebesgut

Integrali i Riemann-it nuk është i përkufizuar për përdorim në gamë të gjerë funksionesh dhe situatash të rëndësishme. Për shembull integrali i Riemann-it mund lehtë të integrojë dendësinë, të gjejë masën e binarit të hekurit, por nuk mund të shtojë dhe vlerat e gjylës së hekurit të vendosur mbi atë binarë. Ky problem nxitë përkufizime tjera, që sjell në pahë dhe përkufizues tjerë si Harv, Rudin etj. Integrali i Lebesgut pjesërisht arrinë fleksibilitet të lartë duke kthyer vëmendjen kah peshat në shumat e peshave.

Përkufizimi i integralit të Lebesgut këtu fillon me masën, μ. Në rastin më të thjeshtë pesha e Lebesgut μ(A) e një intervali A = [a,b] është gjerësia e sajë, b − a, pra në këtë rast integrali i Lebesgut përputhet me integralin e Riemann-it. Në raste më të komplikuara që maten mund të fagmentohen me një numër të lartë fragmentesh pa vazhdueshmëri dhe pa ngjashmëri me intervalet.

Për të shfrytëzuar këtë fleksibilitet integrali i Lebesgut kthen prapa qasjen tek shuma e matur.

Një qasje e përbashkët fillimisht përkufizon integralin e funksionit të indikatorit të mjetit të matur A si vijon:

$\int 1_{A}d\mu =\mu (A)$.

Kjo zgjerohet nga lineariteti në funksion të thjeshtë të matshëm s, i cili arrin vetëm vetm numët të caktuar , n, të vlerave të caktuara jo negative:

${\begin{aligned}\int s\,d\mu &{}=\int \left(\sum _{i=1}^{n}a_{i}1_{A_{i}}\right)d\mu \\&{}=\sum _{i=1}^{n}a_{i}\int 1_{A_{i}}\,d\mu \\&{}=\sum _{i=1}^{n}a_{i}\,\mu (A_{i})\end{aligned}}$

Ku nëse E është mjet i matshëm kemi përkufizimin:

$\int _{E}s\,d\mu =\sum _{i=1}^{n}a_{i}\,\mu (A_{i}\cap E).$

Pastja për çdo funksion të matshëm jo negativ f kemi përkufizimin:

$\int _{E}f\,d\mu =\sup \left\{\int _{E}s\,d\mu \,\colon 0\leq s\leq f{\text{ dhe }}s{\text{ eshte funksion i thjeshte}}\right\};$

Funskioni i përgjithëshëm i matshëm f është ndarë në vlerat e tijë pozitive dhe negative në prkufizimin:

${\begin{aligned}f^{+}(x)&{}={\begin{cases}f(x),&{\text{if }}f(x)>0\\0,&{\text{perndryshe}}\end{cases}}\\f^{-}(x)&{}={\begin{cases}-f(x),&{\text{if }}f(x)<0\\0,&{\text{perndryshe}}\end{cases}}\end{aligned}}$

Përfundimisht f është integlar i Lebesgut nëse:

$\int _{E}|f|\,d\mu <\infty ,\,\!$

dhe pastaj integrali përkufizohet nga:

$\int _{E}f\,d\mu =\int _{E}f^{+}\,d\mu -\int _{E}f^{-}\,d\mu .\,\!$

Pa barazia e integraleve

• Lidhjet e larta dhe të ulta. Një funksion i integrueshëm f në [a, b], është patjetër i lidhur në atë interval. Kështu aty ka numra real m dhe M ashtu që m ≤ f (x) ≤ M për tëgjitha x në [a, b]. Prandaj shumat më të larta dhe më të ulëta të f mbi [a, b] janë të lidhura, respektivisht nga m(b − a) dhe M(b − a), pason:

$m(b-a)\leq \int _{a}^{b}f(x)\,dx\leq M(b-a).$

• Pabarazitë në mes funksioneve. Nëse f(x) ≤ g(x) për çdo x në [a, b] atëherë çdo shumë e lartë dhe e ulët e f është e lidhur mbi nga shuma e lartë dhe e ulët, respektivisht nga g. Kështu kemi:

$\int _{a}^{b}f(x)\,dx\leq \int _{a}^{b}g(x)\,dx.$

Ky është përgjithësim i pabarazive të mësipërme siç është M(b − a), integral i funksionit konstant me verë M mbi [a, b].

• Nënintervalset. Nëse [c, d] është nëninterval i [a, b] dhe f(x) është jo-negativ për tëgjithë vlerat x, atherë kemi:

$\int _{c}^{d}f(x)\,dx\leq \int _{a}^{b}f(x)\,dx.$

• Vlera prouktive dhe absolute e funksioneve. Nëse f dhe g janë dy funksione atëherë mund të kosiderojmë krijimin e një funksioni të tretë dhe vlerën e tyre absolute të tyre:

$(fg)(x)=f(x)g(x),\;f^{2}(x)=(f(x))^{2},\;|f|(x)=|f(x)|.\,$

Nëse f është integral i Riemann-it në [a, b] atëherë i njejti është i saktë për |f|, dhe

$\left|\int _{a}^{b}f(x)\,dx\right|\leq \int _{a}^{b}|f(x)|\,dx.$

Mëtej, nëse f dhe g janë që të dy funksione integrale të Riemann-it atëherë f ², g ², dhe fg janë gjithashtu integrale të Riemann-it, dhe

$\left(\int _{a}^{b}(fg)(x)\,dx\right)^{2}\leq \left(\int _{a}^{b}f(x)^{2}\,dx\right)\left(\int _{a}^{b}g(x)^{2}\,dx\right).$

Ky jo barazim i njohur si jobarazimi Cauchy–Schwarz, luan rol të rëndësishëm në teorinë e hapësirës së Hilbertit ku ana e majtë praqitet si prodhim i brendshëm i dy funksioneve të shesht-integrale f dhe g në intervalin [a, b].

• Jobarazimi i Hölderit. Supozojmë se p dhe q janë numra real, 1 ≤ p, q ≤ ∞ me 1/p + 1/q = 1, dhe f dhe g janë dy funksione integrale të Riemann-it. Pastaj funksionet |f|^p dhe |g|^q janë gjithashtu të integrueshëm, kështu jobarazimi i Hölderit përkufizohet si:

$\left|\int f(x)g(x)\,dx\right|\leq \left(\int \left|f(x)\right|^{p}\,dx\right)^{1/p}\left(\int \left|g(x)\right|^{q}\,dx\right)^{1/q}.$

Për p = q = 2, jobarazimi i Hölderit bëhet jobarazimi i Cauchy–Schwarz.

• Jobarazimi i Minkowskit. Supozojmë se p ≥ 1 është numër real dhe f dhe g janë funksione integrale të Riemann-it. Atëherë kemi: |f|^p, |g|^p dhe |f + g|^p janë gjithashtu integrale të Riemann-it dhe jobarazimi i Minkowskit thotë:

$\left(\int \left|f(x)+g(x)\right|^{p}\,dx\right)^{1/p}\leq \left(\int \left|f(x)\right|^{p}\,dx\right)^{1/p}+\left(\int \left|g(x)\right|^{p}\,dx\right)^{1/p}.$

Në mënyrë analogjike me këtë jobarazim për integralin e Lebesgut është përdorur në konstruktimin e hasirave L^p.

Teoremat themelore të analizës matematike

• Teorema themelore e analizës matematike. Le të jetë f funksion i një integrali të mbyllur [a, b]. Nëse F përkufizohet për x në [a, b] nga

$F(x)=\int _{a}^{x}f(t)\,dt.$

atëherë F është e vazhdueshme në [a, b]. Nëse f është i vazhdueshëm në x në [a, b], atëherë F është i derivueshëm tek x, dhe F ′(x) = f(x).

• Terema e dytë themelore e analizës matematike. Le të jetë f funksion i një integrali të mbyllur [a, b]. Nëse F është funksion si F ′(x) = f(x) për tëgjitha x në [a, b] (kjo do të thotë., F është një kundërderivat i f), atëherë kemi:

$\int _{a}^{b}f(t)\,dt=F(b)-F(a).$

• Corollary. Nëse f është funksion i vazhdueshëm në [a, b], atëherë f është i integrueshëm në [a, b] dhe F, përkufizohet nga:

$F(x)=\int _{a}^{x}f(t)\,dt$

është kundër derivat i f në [a, b]. për më tepër:

$\int _{a}^{b}f(t)\,dt=F(b)-F(a).$

Shikoni edhe

• Matematika
• Analiza matematikore

Lidhje të jashtme

• The Integrator nga Wolfram Research -
• Function Calculator from WIMS -

Libra në internet

• Keisler, H. Jerome, Elementary Calculus: An Approach Using Infinitesimals, University of Wisconsin -
• Stroyan, K.D., A Brief Introduction to Infinitesimal Calculus, University of Iowa -
• Mauch, Sean, Sean's Applied Math Book, CIT, an online textbook that includes a complete introduction to calculus -
• Crowell, Benjamin, Calculus, Fullerton College, an online textbook -
• Garrett, Paul, Notes on First-Year Calculus -
• Hussain, Faraz, Understanding Calculus, an online textbook -
• Sloughter, Dan, Difference Equations to Differential Equations, an introduction to calculus -
• Wikibook of Calculus -
• Numerical Methods of Integration at Holistic Numerical Methods Institute -