Sistemi koordinativ polar

Në matematikë, sistemi koordinativ polar është një sistemin koordinativ dy-dimensional në të cilin çdo pikë në plan jepet nga një distancë nga një pikë e caktuar dhe një kënd nga një drejtim i caktuar.
Pika fikse (në analogji me origjinën e një sistemi kartezian) quhet poli, dhe rrezja nga ky pol me drejtim të caktuar quhet boshti polar. Distanca nga poli quhet koordinata rrezore ose rrezja, kurse këndi quhet koordinata këndore, këndi polar, apo azimuti.[1]
Historia[Redakto | Redakto nëpërmjet kodit]
- Artikulli kryesor: Historia e funksioneve trigonometrike
Konceptet e këndit dhe rrezes përdoreshin nga popujt e lashtë gjatë mijëvjeçarit të parë para lindjes së Krishtit. Astronomi grek Hipparchus (190-120 pes) krijoi një tabelë me funksione kordash që jepte gjatësinë e cdo korde për cdo kend, ka referenca se ai përdori koordinatat polare për të llogaritur pozicionet e yjeve.[2].Në veprën Mbi spiralet, Arkimedi përshkruan spiralen e Arkimedit, një funksion,rrezja etë cilit varet nga këndi. Matematikani grek, megjithatë, nuk e zgjeroi koncpetin në një sistem kordinativ të plotë.
Në shekullin e 9-të, matematikani persian, Habash al-Hasib el-Marwazi, përdori metodat e trigonometrisë sferike dhe projektimin gjeohapësinor në mënyrë që të konvertonte koordinatat polare në një sistem koordinativ të ndryshëm të përqëndruar në një pikë të veçantë mbi sferë, në këtë rast tek Kibla, në drejtim të Mekes.[3] Gjeografi Persian , Abu Rayhān Bīrūnī (973-1048), zhvilloi ide të cilat janë parë si parapritëse të sistemit koordinativ polar.[4] Rreth 1025, ai ishte i pari që përshkroi një projeksion azimutal të baraslarguar polar të sferës qiellore.[5]
Konvencionet e zakonshme[Redakto | Redakto nëpërmjet kodit]

Koordinata rrezore tregohet me simbolin , kurse koordinata këndore me ose t.
Këndet në notacionin polar janë të shprehura në përgjithësi në gradë ose radian (2 π radian është e barabartë me 360°). Gradat janë përdorur tradicionalisht në navigacion, gjeodezi, dhe në shumë disiplina të aplikuara, ndërsa radiani është më i përdorur në matematikë dhe në fizikë matematikore.[6]
Në shumë kontekste, një koordinatë pozitive këndore do të thotë që këndi θ matet në drejtim të kundërt të akrepave të sahatit.
Në literaturën matematikore, boshti polar vizatohet në mënyrë horizontale dhe i treguar në të djathtë.
Uniciteti i koordinatave polare[Redakto | Redakto nëpërmjet kodit]
Shtimi i një numri që paraqet një rrotullim të plotë (360°) tek koordinatat këndore nuk e ndryshon drejtimin përkatës. Gjithashtu, një koordinatë rrezore negative mund të interpretohet më mirë si një distancë përkatëse pozitive e matur në drejtim të kundërt. Prandaj, të njëjtën pikë mund ta shprehim me një numër të pafund koordinatash polare (r, θ ± n×360°) ose (−r, θ ± (2n + 1)180°), ku n është një numër i plotë.[7] Për më tepër, vetë poli koordinativ jepet nga (0, θ) për çdo kënd θ.[8]
Kur një përfaqësim unik është i nevojshme për çdo pikë, zakonisht r kufizohet tek numrat jo-negativ (r ≥ 0) dhe θ në intervalin [0, 360°) ose (−180°, 180°] (në radianë, [0, 2π) ose (−π, π]).[9] Gjithashtu duhet zgjedhur një azimut unik për polin, psh. θ = 0.
Konvertimi midis koordinatave polare dhe atyre Karteziane[Redakto | Redakto nëpërmjet kodit]
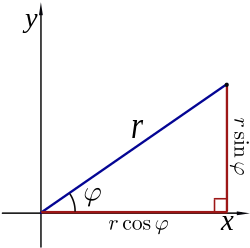
Të dyja koordinatat polare r dhe θ mund të konvertohen në koordinata Karteziane dhe duke përdorur funksionet trigonometrike sinus dhe kosinus :
të dyja koordinatat Karteziane dhe mund të konvertohen në koordinata polare me anë të ekuacioneve
- (si tek teorema e Pitagorës), dhe
Të gjitha këto formula marrin parasysh se poli është origjina Karteziane (0,0), boshti polar është boshti i abshisave , dhe se drejtimin e boshtit i boshtit të ordinatave ka azimut +π/2 rad = +90° (në vend se -π/ 2). Funksioni arcsin është inversi i funksionit sinus , i cili jep kënde në intervalin [−π/2,+π/2] = [−90°,+90°].
Formula për më sipër jep një kënd në intervalin [-π/2,+3π/2) = [−90°,+270°). Për të marrë θ në intervalin [0, 2π) direkt, mund të përdorim
Funskioni është inversi i funksionit tangjent , i cili jep një kënd ne intervalin (−π/2,+π/2) = (−90°,+90°).
Për te marre ne intervalin (−π, π], mund te përdorim [10]
Shume gjuhe programimi kane një funksion i cili llogarit koordinatën këndore korrekte θ po te kemi x dhe y, pa bere analizene e mëlartme. Për shembull, ky funksion thirret nga atan2(y,x) ne gjuhen e programimit C, dhe (atan y x) ne Lisp. Ne te dyja rastet, rezultati është ne radian ne intervalin (−π, π].
Ekuacioni polar i një kurbe[Redakto | Redakto nëpërmjet kodit]
Ekuacioni që përcakton një kurbë algjebrike i shprehur në koordinata polare është i njohur si një ekuacion polar . Në shumë raste, ky ekuacion thjesht mund të specifikohet duke përcaktuar r si një funksion funksion të . Kurbë rezultante përbëhet nga pika të formës dhe mund të konsiderohet si grafiku i funksionit polar r.
Format e ndryshme të simetrisë mund të merrent nga ekuacioni i një funksioni polare . Nëse kurba do të jetë simetrike në lidhje me rrezen horizontale (0°/180°), nëse ajo do të jetë simetrike në lidhje me rrezen vertikale (90°/270°), dhe nëse ajo do të jetë simetrike α në drejtimi të kundërt të akrepave të sahati në lidhje me polin.
Për shkak të natyrës rrethore të sistemit koordinativ polar, shumë kurba mund të përshkruhen me një ekuacion tepër të thjeshtë polare, ndërsa forma e tyre Kartezian është shumë më e ndërlikuar. Në mes të kurbave më të njohura janë trëndafili polare, spiralja e Arkimedit, lemniskata, limaçon, dhe kardioidi .
Për rrethin, vijën, dhe trëndafilin polare më poshtë, kuptohet se nuk ka kufizime në fushën dhe rangun e përcaktimit.
Rrethi[Redakto | Redakto nëpërmjet kodit]
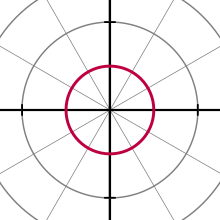
Ekuacioni i përgjithshëm për një rreth me qendër në dhe rreze është
Kjo mund të thjeshtohet në mënyra të ndryshme, në përputhje me rastet më specifike, të tilla si ekuacioni
për një rreth me qendër në pole dhe rreze a.[11]
Vija[Redakto | Redakto nëpërmjet kodit]

Vijat radiale (ato që kalojnë përmes polit) paraqiten nga ekuacioni
- ,
ku është këndi i ngritjes të vijës; pra, ku m është pjerrësia e vijës në sistemin koordinativ Kartezian. Vijat jo-rrezore që kryqëzohen me vijën radiale pingul tek pika kanë ekuacionin
Trëndafili polar[Redakto | Redakto nëpërmjet kodit]
Një trëndafili polar është një kurbë e famshme matematike që duket si një petal luleje, që mund të shprehet me anë të një ekaucioni të thjeshtë polar,
për çdo konstante (përfshirë 0). Nëqoftëse është një numër i plotë , këto ekuacione do të japin një trëndafil me -petale nëqoftëse është tek, ose një trëndafil me 2 -petale nëqoftëse është çift. Nëqoftëse është numër thyesor por jo numër i plotë, do të marrim një formë që i ngjason trëndafilit por me petale që janë mbi njëri tjetrin. Vini re se këto ekuacione kurrë nuk përcaktojnë një trëndafil me 2, 6, 10, 14, etc. petale. Ndryshorja a paraqet gjatësinë e petaleve të trëndafilit.
Spiralja e Arkimedit[Redakto | Redakto nëpërmjet kodit]

Spiralja e Arkimedit është një spirale e famshme që u zbulua nga Arkimedi, e cili mund të shprehet me anë të një ekuacioni të thjeshtë polar. Ajo është e përfaqësuar nga ekuacioni
Ndryshimi i parametër a e ndryshon drejtimin e spirales, ndërsa b kontrollon distanca në mes të krahëve, të cilat për një spirale të caktuar janë gjithmonë konstante. Spiralja e Arkimedit ka dy krahë, një për dhe një për . Të dyja krahët janë të lidhura tek poli. Po të marrim imazhin pasqyrë të një krahu përgjatë vijës 90° / 270° marrim krahun tjetër. Kjo kurbë është e famshme për faktin se qe një nga kurbat e para, pas seksioneve konike , e cila u përshkrua në një traktat matematikor, dhe si një shembull kryesor i një kurbe që është e përcaktuar më mirë nga një ekuacion polar (në krahasim me formën karteziane).
Prerjet konike[Redakto | Redakto nëpërmjet kodit]
- Artikulli kryesor: Prerjet konike
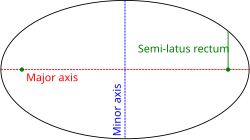
Një prerje konike me një vatër në njërin pol dhe tjetrën diku në një rreze që fillon nga 0° (në mënyrë që boshti madhor i konikut shtrihet përgjatë boshtit polar) jepet nga :
ku e është jashtëqëndërsia dhe është semi-latus rectum (distanca pingule nga vatra tek boshti madhor i kurbës). Nëqoftëse e > 1, ky ekaucion përcakton një hiperbolë; nëqoftëse e = 1, ai përcakton një parabolë; dhe nëqoftëse e < 1, ai përcakton një elips. Rsti special i e = 0 rastit të lartëm rezulton në një rreth me rreze .
Numrat kompleks[Redakto | Redakto nëpërmjet kodit]
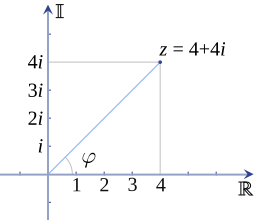
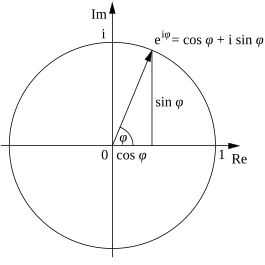
Çdo numër kompleks mund të paraqitet si një pikë në planin kompleks, kështu që ajo mund të shprehet ose duke specifikuar koordinatat e pikës karteziane (kjo quhet forma Karteziane) ose koordinatat polare të pikës (kjo quhet forma polare). Numri kompleks mund të paraqitet në formë karteziane si
ku i është njësia imagjinare, ose në mënyrë alternative mund të shkruhet në formë polare (përmes formulës së konvertimit e dhënë më lart) si
si dhe
ku e është numri i Ojlerit, të cilat janë të njëvlershme siç tregohet nga formula e Ojlerit.[12] (Vini re se kjo formulë, si të gjitha ato që përfshijnë eksponente këndesh, merr parasysh që këndi θ është shprehur në radian.) Në mënyrë që të konvertojmë midis formës polare dhe karteziane të një numri kompleks, formula e konvertimit më lart mund të përdoret.
Për veprimet e shumëzimit, pjesëtimit, dhe ngritjes në eksponent të numrave kompleksë, në përgjithësi është më e lehtë të punohet me numra kompleksë t shprehur në formë polare krahasuar me formë Karteziane. nga ligji i ngritjes në eksponent:
- Shumëzimi:
- Pjestimi:
- Ngritja në eksponent (Forumala e De Moivre):
Analiza[Redakto | Redakto nëpërmjet kodit]
Teknikat e analizës mund të zbatohen mbi ekuacionet e shprehura në koordinata polare.[13][14]
Koordinata polare θ është shprehur në radian përgjatë këtij seksioni, kjo paraqet konvencionin e zakonshëm në përdorimin e analizës.
Analiza diferenciale[Redakto | Redakto nëpërmjet kodit]
Po të përdorim dhe , ne mund të derivojmë një relacion midis derivateteve në koordinata polare dhe Karteziane. Për një funksion të dhënë , , del se
ose
Nga kjo marrim formulën e mëposhtme:
Për të gjetur pjerrësinë Karteziane të një vije tangjente me kurbën polare në çdo pikë të dhënë, kurba jepet si një sistem ekuacionesh parametrike.
Duke diferencuar të dyja ekuacionet në lidhje me θ marrim
Po të pjesëtojmë ekuacionin e dytë me të parin marrim pjerrësinë Karteziane të vijës tangjente me kurbën tek pika :
Analiza integrale[Redakto | Redakto nëpërmjet kodit]
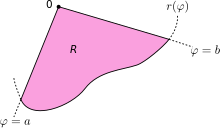
Le të shënojmë me rajonin e rrethuar nga një kurbë dhe rrezet dhe , ku . Sipërfaqja e është
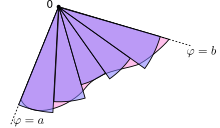

Ky rezultat mund të gjendet si më poshtë. Së pari, intervali [a, b] është i ndarë në n nën-intervale, ku n është një numër i plotë pozitiv arbitrar. Kështu , gjatësia e çdo nën-intervali, është e barabartë me b − a (kohëzgjatja e përgjithshme e intervalit), e ndarë sipas n, numri i nën-intervaleve . Për çdo nën-interval i= 1, 2, ...,n, le të jetë pika e mesit e nën-intervalit, tani le të ndërtojmë një sektor rrethor me qendër në pole, rreze r(θi),,kënd qendrore Δθ dhe gjatësi harku r(θi)Δθ.. Zona e secilit sektor të ndërtuar është e barabartë me
Kështu, zona e përgjithshme e të gjithë sektorëve është
Ndërsa numri i nën-intervaleve n rritet, përafrimi i zonës vazhdon të përmirësohet. Në kufirin kur , shuma bëhet shuma Rimaniane për integralin e mëlartëm.
Një pajisje mekanike që llogarit integrale sipërfaqësore është planimetri, i cili mat fushën e një plani: kjo replikon integrimin në koordinatat polare duke shtuar shfrytëzuar teoremën e Greenit, çka bën konvertimin e integrale kuadratike polare në integrale lineare.
Përgjithësime[Redakto | Redakto nëpërmjet kodit]
Duke përdorur koordinatat Karteziane, një element infinitezimal i sipërfaqes mund të llogaritet si dA = dx dy. Rregulli i zëvendësimit për integrale të shumëfishta pohon se, kur përdorim koordinata të tjera, përcaktori Jakobian i formulës së konvertimit të koordinatave duhet të merret në konsidertaë:
Pra, një element sipërfaqësor në koordinata polare mund të shkruhet si
Tani , një funksion që është i dhënë në koordinata polare mund të integrohet si më poshtë:
Këtu , R është i njëjti rajon si më lartë, pra, rjoni i rrethuar nga kurba r(θ) dhe rrezet θ = a dhe θ = b.
Formula për sipërfaqen e R e përmendur më lart gjendet duke marrë f identikisht të barabartë me 1. Një zbatim interesant i këtij rezultati jep integralin Gausian
Analiza vektoriale[Redakto | Redakto nëpërmjet kodit]
Analiza vektoriale mund të zbatohet gjithashtu mbi koordinatat polare. Për lëvizjen në një plan , le të jetë vektori i pozicionit , ku r dhe θ kanë varësi kohore t.
Le të përcaktojmë vektorët njësi
në drejtimin e r dhe
në planin e lëvizjes pingul me drejtimin rrezor, ku është vektori njësi pingul me planin e lëvizjes.
Pra
ku h është impulsi këndor specifik.
Termat centrifugale dhe termat e Koriolisit[Redakto | Redakto nëpërmjet kodit]
- Artikuj kryesore: Mekanika e lëvizjes planare të pikës lëndore
Termi zakonisht quhet termi centrifugal, ndërsa termi referohet si termi i Koriolisit. Për shembull, shih Shankar.[15] Edhe pse këto ekuacione mbajnë disa ngjashmëri në formë me forcën centrifugale dhe efektin e Koriolisit që gjenden në kënde reference në rrotullim, nuk ka një lidhje fizike midis këtyre fenomeneve.[16] Për shembull, forca centrifugale dhe ajo e Koriolisit shfaqen vetëm në kënde reference joinerciale të referimit. Në të kundërt, këto terma shfaqen kur nxitimi është shprehur në koordinatat polare janë rrjedhoja matematike të diferencimit, këto terma duken kudo ku janë përdorur koordinatat polare. Në veçanti, këto terma duken edhe kur koordinatat polare janë përdorur në kënde inerciale të referimit , ku nuk shfaqen forcat centrifugale dhe efekti i Koriolisit.
Sistemet bashkë-rrotulluese[Redakto | Redakto nëpërmjet kodit]
Lidhja midis koordinatave sferike dhe polare[Redakto | Redakto nëpërmjet kodit]
Koncepti i sistemit koordinativ polar zgjerohet në tre dimensione me dy sisteme të tjera koordiantive, sistemin koorinativ sferik dhe atë cilindrik.
Aplikime[Redakto | Redakto nëpërmjet kodit]
Koordinatat polare janë dy-përmasore dhe në këtë mënyrë ato mund të përdoren vetëm ku pozicionet e pikave shtrihen në një plan të vetëm dy-dimensional. Ato janë më të përshtatshme në çdo kontekst ku fenomen i marrë në konsideratë është i lidhur me drejtimin dhe gjatësine nga një pikë qëndrore. Siç duket, shembujt më lart tregojnë se si ekuacionet polare elementare mjaftojnë për të përcaktuar kurba të tilla si spiralja e Arkimedit ekuacioni i të cilit në sistemin koordinativ Kartezian do të ishte shumë më i ndërlikuar. Për më tepër, shumë sisteme fizike, të tilla si ato që kanë të bëjnë me trupa që lëvizin rreth një pikë qendrore apo me fenomene që rrjedhin nga një pikë qendrore janë më të thjeshta dhe më të kuptueshëm për tu modeluar duke përdorur koordinatat polare. Motivimi fillestar për futjen e sistemit polar ishte studimi i lëvizje rrethore dhe asaj orbitale.
[Redakto | Redakto nëpërmjet kodit]
Modelimi[Redakto | Redakto nëpërmjet kodit]
Shikoni gjithashtu[Redakto | Redakto nëpërmjet kodit]
Referime[Redakto | Redakto nëpërmjet kodit]
- Të Përgjithshme
- Anton Howard; Irl Bivens; Stephen Davis (2002). Calculus (bot. Seventh). Anton Textbooks, Inc. ISBN 0-471-38157-8.
{{cite book}}: Mungon ose është bosh parametri|language=(Ndihmë!) - Ross Finney; George Thomas; Franklin Demana; Bert Waits (1994). Calculus: Graphical, Numerical, Algebraic (bot. Single Variable Version). Addison-Wesley Publishing Co. ISBN 0-201-55478-X.
{{cite book}}: Mungon ose është bosh parametri|language=(Ndihmë!)
- Specifike
- ^ Brown, Richard G. (1997). Andrew M. Gleason (red.). Advanced Mathematics: Precalculus with Discrete Mathematics and Data Analysis. Evanston, Illinois: McDougal Littell. ISBN 0-395-77114-5.
{{cite book}}: Mungon ose është bosh parametri|language=(Ndihmë!) - ^ Friendly, Michael. "Milestones in the History of Thematic Cartography, Statistical Graphics, and Data Visualization". Arkivuar nga origjinali më 20 mars 2011. Marrë më 2006-09-10.
{{cite web}}: Mungon ose është bosh parametri|language=(Ndihmë!) - ^ T. Koetsier, L. Bergmans (2005). Mathematics and the Divine. Elsevier. fq. 169. ISBN 0444503285.
{{cite book}}: Mungon ose është bosh parametri|language=(Ndihmë!) - ^ Stampa:MacTutor
- ^ David A. King (1996), "Astronomy and Islamic society: Qibla, gnomics and timekeeping", in Roshdi Rashed (ed.), Encyclopedia of the History of Arabic Science, Vol. 1, pp. 128–184 [153], Routledge, London and New York
- ^ Raymond A. Serway; Jewett, Jr.; John W. (2005). Principles of Physics. Brooks/Cole—Thomson Learning. ISBN 0-534-49143-X.
{{cite book}}: Mungon ose është bosh parametri|language=(Ndihmë!) - ^ "Polar Coordinates and Graphing" (PDF). 2006-04-13. Arkivuar nga origjinali (PDF) më 15 shkurt 2012. Marrë më 2006-09-22.
{{cite web}}: Mungon ose është bosh parametri|language=(Ndihmë!) - ^ Theodore Lee; David Cohen; David Sklar (2005). Precalculus: With Unit-Circle Trigonometry (bot. Fourth). Thomson Brooks/Cole. ISBN 0534402305.
{{cite book}}: Mungon ose është bosh parametri|language=(Ndihmë!) - ^ Ian Stewart; David Tall (1983). Complex Analysis (the Hitchhiker's Guide to the Plane). Cambridge University Press. ISBN 0521287634.
{{cite book}}: Mungon ose është bosh parametri|language=(Ndihmë!) - ^ Bruce Follett Torrence; Eve Torrence (1999). The Student's Introduction to Mathematica. Cambridge University Press. ISBN 0521594618.
{{cite book}}: Mungon ose është bosh parametri|language=(Ndihmë!) - ^ Claeys, Johan. "Polar coordinates". Arkivuar nga origjinali më 2 mars 2000. Marrë më 2006-05-25.
{{cite web}}: Mungon ose është bosh parametri|language=(Ndihmë!) - ^ Smith, Julius O. (2003). "Euler's Identity". Mathematics of the Discrete Fourier Transform (DFT). W3K Publishing. ISBN 0-9745607-0-7. Arkivuar nga origjinali më 15 shtator 2006. Marrë më 2006-09-22.
{{cite book}}: Mungon ose është bosh parametri|language=(Ndihmë!) - ^ Husch, Lawrence S. "Areas Bounded by Polar Curves". Arkivuar nga origjinali më 1 mars 2000. Marrë më 2006-11-25.
{{cite web}}: Mungon ose është bosh parametri|language=(Ndihmë!) - ^ Lawrence S. Husch. "Tangent Lines to Polar Graphs". Arkivuar nga origjinali më 21 nëntor 2019. Marrë më 2006-11-25.
{{cite web}}: Mungon ose është bosh parametri|language=(Ndihmë!) - ^ Ramamurti Shankar (1994). Principles of Quantum Mechanics (bot. 2nd). Springer. fq. 81. ISBN 0306447908.
{{cite book}}: Mungon ose është bosh parametri|language=(Ndihmë!) - ^ Në veçanti, shpejtesia kendore e paraqitur në kordinata polare është ajo e grimcës nën vëzhgim, , ndërsa në mekanikën klasike te Njutonit është shpejtesia kendore Ω shkalla e një kendi reference ne rrotullim.





























































![{\displaystyle {\frac {1}{2}}\int _{a}^{b}\left[r(\theta )\right]^{2}\,d\theta .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/172b9297fd20229b4df6fbb675e5a30721127f1e)



![{\displaystyle \left[r(\theta _{i})\right]^{2}\pi \cdot {\frac {\Delta \theta }{2\pi }}={\frac {1}{2}}\left[r(\theta _{i})\right]^{2}\Delta \theta .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1273733d787cac63ac635e3c69e09b6021bd3479)

















