Hapësira tre-dimensionale

A representation of a three-dimensional Cartesian coordinate system with the x-axis pointing towards the observer

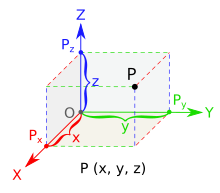
Në gjeometri, një hapësirë tre-dimenzionale (hapësirë 3D apo rrallë hapësirë tri-dimenzionale) është një hapësirë matematikore në të cilën kërkohen tre vlera (koordinata) për të përcaktuar pozicionin e një pike. Më së shpeshti, është hapësira Euklidiane tre-dimenzionale, domethënë hapësira Euklidiane e dimensionit tre, që modelon hapësirën fizike. Hapësirat më të përgjithshme tre-dimensionale quhen 3-manifold. Termi mund t'i referohet gjithashtu në mënyrë bisedore një nëngrupi hapësire, një rajoni tredimensional (ose domeni 3D), një figurë solide.

Teknikisht, një tufë n numrash mund të kuptohen si koordinatat karteziane të një vendndodhjeje në një hapësirë Euklidiane n-dimensionale. Bashkësia e këtyre n-tupave zakonisht shënohet 𝑅𝑛 dhe mund të identifikohet në çiftin e formuar nga një hapësirë Euklidiane n-dimensionale dhe një sistem koordinativ kartezian. Kur n = 3, kjo hapësirë quhet hapësira Euklidiane tredimensionale (ose thjesht "hapësirë Euklidiane" kur konteksti është i qartë). Në fizikën klasike, ai shërben si një model i universit fizik, në të cilin ekziston e gjithë materia e njohur. Kur merret parasysh teoria e relativitetit, ajo mund të konsiderohet një nënhapësirë lokale e hapësirë-kohës. Ndërsa kjo hapësirë mbetet mënyra më bindëse dhe e dobishme për të modeluar botën ashtu siç përjetohet, është vetëm një shembull i një larmie të madhe hapësirash në tre dimensione të quajtura 3-manifold. Në këtë shembull klasik, kur të tre vlerat i referohen matjeve në drejtime të ndryshme (koordinata), mund të zgjidhen çdo tre drejtime, me kusht që këto drejtime të mos shtrihen në të njëjtin rrafsh. Për më tepër, nëse këto drejtime janë pingul në çift, të tre vlerat shpesh etiketohen me termat gjerësi/gjerësi, lartësi/thellësi dhe gjatësi.

Shiko edhe

• Hapësira një-dimenzionale
• Hapësira dy-dimenzionale
• Hapësira katër-dimenzionale