Numri kompleks

Numri kompleks është përgjithësim i numrit real me ndihmën e një numri special i cili shënohet me i dhe quhet njësi imagjinare i cili sipas përkufizimit e plotëson kushtin

$i^{2}=-1.\,$

Numrat kompleks në fillim u zbuluan nga matematikani italian Girolamo Cardano, gjatë përpjekjeve të tij për gjetjen e zgjidhjeve të Ekuacionit të shkallës së tretë. Rregullat për shumën, ndryshimin, shumëzimin dhe pjestimin e numrave kompleks u dhanë nga mattematikani italian Rafael Bombelli. Një formalizëm më apstrakt për numrat kompleks më vonë ndërtoi matematikani irlandez William Rowan Hamilton, i cili konceptin e numrit kompleks e zgjëroi edhe më tej dhe në matematikë futi konceptin e kuaternioneve.

Përkufizimi

Bashkësia e numrave kompleks shënohet me C, ndërsa numri kompleks në trajtën

$a+bi\,$

ku $a\,$ dhe $b$ janë numra real dhe $i\,$ njësia imagjinare e cila e plotëson vetinë :$i^{2}=-1.\,$. Numri real $a$ është pjesa reale dhe $b$ është pjesa imagjinare.

P.sh. për numrin kompleks 3 + 2i numri 3 është pjesa reale dhe 2 është pjesa imagjinare. Nëse $z=a+bi$, atëherë zakonisht shënojmë a = Re(z) dhe b = Im(z)

Bashkësia e numrave real R mund të kuptohet si nënbashkësi e bashkësisë së numrave kompleks C sepse ç'do numër real mund të shkruhet si numër kompleks i cili pjesën imagjinare e ka të barabartë me 0.

Përkufizimi formal

Është e papranueshme rigorozisht që thjesht të supozojmë se ekziston një lloj numri katrori i të cilit është i barabartë me -1. Përkufizimi i tillë është intuitiv ne më poshtë do të japim përkufizimin formal apo aksiomatik. Themi se bashkësia e numrave kompleks është bashkësi e dysheve të renditura të numrave real e cila në lidhje me mbledhjen dhe shumëzimin e këtyre dysheve të renditura i plotëson kushtet

(a, b) + (c, d) = (a + c, b + d)

(a, b)·(c, d) = (a·c − b·d, b·c + a·d)

Pasi sipas përkufizimit të shumëzimit vlen se (0, 1)·(0, 1) = (−1, 0), ne e gjejmë i në mënyrë konstruktive duke ia shoqëruar atij dyshen e renditur (0, 1). Numrit real $a$ ia shoqërojmë dyshen (a, 0) dhe numrit real $b$ ia shoqërojmë dyshen e renditur (0, b) prandaj në përgjithësi kemi

(a, b) =(a, 0)+(0, b)= a + ib.

Paraqitja gjeometrike e numrave kompleks

Paraqitja gjeometrike e $z$ dhe të konjuguarit të tij ${\bar {z}}$ në rrafshin kompleks.

Sipas përkufizimit të numrit kompleks si dyshe e renditur konkludojmë se numri kompleks mund të shikohet si pikë në rrafsh koordinativ këndrejt të cilin e quajmë rrafsh kompleks. Koordinatat e numrit janë x = Re(z) dhe y = Im(z)

Vlera absolute ose moduli i numrit kompleks

Vlerë absolute ose modul i numrit kompleks $z=x+yi$, është $|z|={\sqrt {x^{2}+y^{2}}}.$

Vetitë kryesore janë:

$|z|\geq 0,\,$ ku $|z|=0\,$ , poqese $z=0\,$

$|z+w|\leq |z|+|w|\,$ (Jobarazimi i trekëndëshit)

$|z\cdot w|=|z|\cdot |w|\,$

Konjugacioni

I konjuguar i numrit kompleks $z=x+yi$ është numri $x-yi$, shënojmë ${\bar {z}}$. Sipas figurës, ${\bar {z}}$ është simetrik me z ndaj boshtit $x$

Disa nga vetitë e konjugacionit:

${\overline {z+w}}={\bar {z}}+{\bar {w}}$

${\overline {z\cdot w}}={\bar {z}}\cdot {\bar {w}}$

${\overline {(z/w)}}={\bar {z}}/{\bar {w}}$

${\bar {\bar {z}}}=z$

$\operatorname {Re} \,(z)={\tfrac {1}{2}}(z+{\bar {z}})$

$\operatorname {Im} \,(z)={\tfrac {1}{2i}}(z-{\bar {z}})$

$|z|=|{\bar {z}}|$

$|z|^{2}=z\cdot {\bar {z}}$

$z^{-1}={\frac {\bar {z}}{|z|^{2}}}$   ku z është i ndryshëm nga 0

Forma polare e numrit kompleks

Figura 2: Argumenti φ dhe moduli r e përcaktojnë pozitën e pikës në një diagram të Arg dhe; $r(\cos \phi +i\sin \phi )$ ose $re^{i\phi }$ janë format polare për paraqitjen e pikës gjegjësisht numrit kompleks.

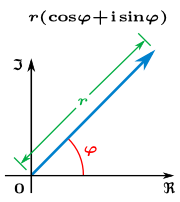
Diagrami nga figura djathtas sugjeron veti të ndryshme.

• Së pari distanca e pikës z nga origjina (i shënuar me r në figurën 2) njihet si vlerë absolute ose modul dhe shënohet me $|z|$. Nga Teorema e Pitagorës,

$|x+iy|={\sqrt {x^{2}+y^{2}}}.$

Në përgjithësi largësia mes numrave kompleks jepet me $d(z,w)=|z-w|$, e cila e kthen bashkësinë e numrave kompleks në hapësirë metrike dhe këtu mund të fusim konceptin e limitit dhe të vazhdueshmërisë së funksioneve. Të gjitha vetitë standarde të hapësirës dydimensionale plotësohen për rrafshin kompleks duke përfshirë atë se moduli i numrit kompleks është jonegativ dhe plotësimin e jobarazimit të trkëndëshit ($|z+w|\leq |z|+|w|$ for all z, w).

• Së dyti argumenti i numrit kompleks $z=x+yi$ është këndi φ i dhënë në figurën 2, shënohet si $\arg(z)$. Si edhe me modulin argumenti mund të gjindet nga $x+iy$:

$\varphi =\pm \arctan {\frac {y}{x}}$ pra $x+iy=\cos \phi +i\sin \phi$).

Vlera e φ ndryshon për një shumfish të 2π dhe përsëri jep këndin e njejtë.

Së bashku këto spjegime japin një mënyrë të re për paraqitjen e numrit kompleks në formën polare, si kombinim i vlerës së modulit këndit që ai formon me boshtin x $(x,y)=(r\cos \varphi ,r\sin \varphi )$ from the polar pair (r,φ)). Këto fakte mund të shënohen në mënyra të ndryshme si p.sh

$z=r(\cos \varphi +i\sin \varphi )\,$

forma trigonometrike, dhe sipas Formulës së Eulerit

$z=re^{i\varphi },$

e cila quhet forma eksponenciale.

Operacionet në formën polare

Operacionet si Shumëzimi, pjestimi fuqizimi dhe rrënjëzimi kur një numër kompleks është shënuar në formën polare janë mjaft të thjeshta:

• Shumëzimi

$(r_{1}e^{i\varphi _{1}})\cdot (r_{2}e^{i\varphi _{2}})=(r_{1}r_{2})e^{i(\varphi _{1}+\varphi _{2})}$

• Pjestimi

${\frac {(r_{1}\,e^{i\varphi _{1}})}{(r_{2}\,e^{i\varphi _{2}})}}=\left({\frac {r_{1}}{r_{2}}}\right)\,e^{i(\varphi _{1}-\varphi _{2})}.$

• Fuqizimi

Fuqizimi i numrit kompleks me një eksponent numër të plotë n bëhet sipas formulës:

$(r(\cos \varphi +i\sin \varphi ))^{n}=r^{n}\,(\cos n\varphi +i\sin n\varphi )$ .........Formula e De Moivreit

• Rrënjëzimi

Rrënjëzimi i numrit kompleks në formën polare gjithashtu është mjaft i thjeshtë. Ç'do numër kompleks z i cili e plotëson barazimin zⁿ = c (për n numër i plotë pozitiv) quhet rrënja e ntë e numrit kompleks c. Nëse c nuk është i barabartë me 0, atëherë ekzistojnë gjithsejt n rrënjë të nta të numrit c. Le të jetë c = re ^iφ dhe $r>0$; atëherë bashkësia e rrënjëve të nta të c është:

$\left\{{\sqrt[{n}]{r}}\,e^{i\left({\frac {\varphi +2k\pi }{n}}\right)}\mid k\in \{0,1,\ldots ,n-1\}\,\right\},$

këtu ${\sqrt[{n}]{r}}$ paraqet rrënjën e ntë numrit real r. Nëse c = 0, atëherë e vetmja rrënjë e ntë e c është vetë 0. Vërejmë se rrënjët ndryshojnë vetëm për një rrotullim për një kënd prej $e^{2k\pi i/n}$, rrënjët e nta të njëshit pra të gjitha rrënjët e c i takojnë një rreti me qendër në origjinën e sistemit koordinativ.

Lidhje të jashtme

• Euler's work on Complex Roots of Polynomials
• John and Betty's Journey Through Complex Numbers
• MathWorld articles Complex number and Argand Diagram, and demonstration "Argand Diagram".
• Dimensions: a math film. Kapitulli 5 jep një hyrje në aritmetikën komplekse dhe për projeksionin stereografik. Kapitulli 6 diskuton për transformimet e rrafshit kompleks.