Shpërndarja Lévy

Lévy

Probability density function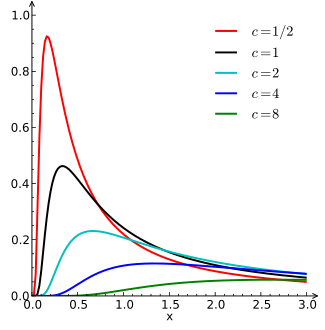
Cumulative distribution function
Mbështetës	$x\in (\mu ,\infty )$
Kuantili	$\mu +{\frac {\sigma }{2\left({\textrm {erfc}}^{-1}(p)\right)^{2}}}$
Vlera e pritur	$\infty$
Mediana	$\mu +c/2({\textrm {erfc}}^{-1}(1/2))^{2}\,$
Moda	$\mu +{\frac {c}{3}}$
Varianca	$\infty$
Shtrirja	e papërcaktuar
Kurtoza e tepërt	e papërcaktuar
Entropia	${\frac {1+3\gamma +\ln(16\pi c^{2})}{2}}$ ku $\gamma$ është konstantja Euler-Maskeroni

Në teorinë e probabilitetit dhe statistikë, shpërndarja Lévy, e quajtur sipas Paul Lévy, është një shpërndarje e vazhduar probabiliteti për një ndryshore të rastit jo-negative. Në spektroskopi, kjo shpërndarje, me frekuencë si ndryshore e varur, njihet si një profil van der Waals . Është një rast i veçantë i shpërndarjes inverse-gama . Është një shpërndarje e qëndrueshme .

Përkufizimi

Funksioni i dendësisë së probabilitetit të shpërndarjes Lévy mbi domenin $x\geq \mu$ është

$f(x;\mu ,c)={\sqrt {\frac {c}{2\pi }}}~~{\frac {e^{-{\frac {c}{2(x-\mu )}}}}{(x-\mu )^{3/2}}}$

ku $\mu$ është parametri i vendndodhjes dhe $c$ është parametri i shkallës . Funksioni i shpërndarjes mbledhëse është

$F(x;\mu ,c)={\textrm {erfc}}\left({\sqrt {\frac {c}{2(x-\mu )}}}\right)=2-2\Phi \left({\sqrt {\frac {c}{(x-\mu )}}}\right)$

ku ${\textrm {erfc}}(z)$ është funksioni i gabimit plotësues dhe $\Phi (x)$ është Funksioni i Laplasit. Parametri i zhvendosjes $\mu$ ka efektin e zhvendosjes së kurbës djathtas me një madhësi $\mu$, dhe ndryshimin e bashkësisë së përcaktimit në intervalin [ $\mu$, $\infty$ ). Ashtu si të gjitha shpërndarjet e qëndrueshme, shpërndarja Levy ka një formë standarde f(x;0,1) e cila ka vetinë e mëposhtme:

$f(x;\mu ,c)dx=f(y;0,1)dy\,$

ku y përkufizohet si

$y={\frac {x-\mu }{c}}\,$

Funksioni karakteristik i shpërndarjes Lévy jepet nga

$\varphi (t;\mu ,c)=e^{i\mu t-{\sqrt {-2ict}}}.$

Vini re se funksioni karakteristik mund të shkruhet gjithashtu në të njëjtën formë të përdorur për shpërndarjen e qëndrueshme me $\alpha =1/2$ dhe $\beta =1$ :

$\varphi (t;\mu ,c)=e^{i\mu t-|ct|^{1/2}~(1-i~{\textrm {sign}}(t))}$

Duke supozuar $\mu =0$, momenti i n i shpërndarjes së pazhvendosur Lévy përcaktohet nga:

$m_{n}\ {\stackrel {\mathrm {def} }{=}}\ {\sqrt {\frac {c}{2\pi }}}\int _{0}^{\infty }{\frac {e^{-c/2x}\,x^{n}}{x^{3/2}}}\,dx$

e cila ndryshon për të gjithë $n\geq 0.5$ në mënyrë që momentet e plota të shpërndarjes Lévy të mos ekzistojnë.

Shpërndarja standarde Lévy plotëson kushtin e të qenit e qëndrueshme

$(X_{1}+X_{2}+\dotsb +X_{n})\sim n^{1/\alpha }X$ ,

ku $X_{1},X_{2},\ldots ,X_{n},X$ janë ndryshore standarde të pavarura Lévy me $\alpha =1/2$ .

Shpërndarjet e ndërlidhura

• Nëse $X\,\sim \,{\textrm {Levy}}(\mu ,c)$ atëherë $kX+b\,\sim \,{\textrm {Levy}}(k\mu +b,kc)$
• Nëse $X\,\sim \,{\textrm {Levy}}(0,c)$ atëherë $X\,\sim \,{\textrm {Inv-Gamma}}({\tfrac {1}{2}},{\tfrac {c}{2}})$ ( shpërndarja e anasjelltë gama ). Këtu, shpërndarja Lévy është një rast i veçantë i një shpërndarjeje të tipit V Pearson
• Nëse $\,Y\,\sim \,{\textrm {Normal}}(\mu ,\sigma ^{2})$ ( Shpërndarja normale ) atëherë ${(Y-\mu )}^{-2}\,\sim \,{\textrm {Levy}}(0,1/\sigma ^{2})$
• Nëse $X\,\sim \,{\textrm {Normal}}(\mu ,{\tfrac {1}{\sqrt {\sigma }}})$ atëherë ${(X-\mu )}^{-2}\,\sim \,{\textrm {Levy}}(0,\sigma )$
• Nëse $X\,\sim \,{\textrm {Levy}}(\mu ,c)$ atëherë $X\,\sim \,{\textrm {Stable}}(1/2,1,c,\mu )$ ( Shpërndarje e qëndrueshme )
• Nëse $X\,\sim \,{\textrm {Levy}}(0,c)$ atëherë $X\,\sim \,{\textrm {Scale-inv-}}\chi ^{2}(1,c)$ ( Shpërndarja e shkallëzuar-inverse-chi-katrore )
• Nëse $X\,\sim \,{\textrm {Levy}}(\mu ,c)$ atëherë ${(X-\mu )}^{-{\tfrac {1}{2}}}\sim \,{\textrm {FoldedNormal}}(0,1/{\sqrt {c}})$ ( Shpërndarja normale e palosur )

Zbatimet

• Frekuenca e përmbysjeve gjeomagnetike duket se ndjek një shpërndarje Lévy
• Koha e goditjes së një pike të vetme, në distancë $\alpha$ nga pika e fillimit, nga lëvizja Brauniane ndjek shpërndarjen Lévy me $c=\alpha ^{2}$ . (Për një lëvizje Brauniane me zhvendosje, këtë herë mund të ndjekë një shpërndarje të anasjelltë Gaussian, e cila ka shpërndarjen Lévy si kufi. )
• Gjatësia e shtegut të ndjekur nga një foton në një mjedis të turbullt ndjek shpërndarjen Lévy.
• Një proces Cauchy mund të përkufizohet si një lëvizje Brauniane e varur nga një proces i lidhur me një shpërndarje Lévy.