Ndryshorja e rastit komplekse

Në teorinë e probabilitetit dhe statistikë, ndryshoret e rastit komplekse janë një përgjithësim i ndryshoreve të rastit me vlerë reale në numra kompleksë, dmth. vlerat e mundshme që mund të marrë një ndryshore e rastit komplekse janë numra kompleksë. Ndryshoret e rastit komplekse mund të konsiderohen gjithmonë si çifte të ndryshoreve të rastit reale: pjesët e tyre reale dhe imagjinare. Prandaj, shpërndarja e një ndryshoreje komplekse të rastit mund të interpretohet si shpërndarja e përbashkët e dy ndryshoreve të rastit reale.

Zbatimet e ndryshoreve të rastit komplekse gjenden në përpunimin numerik të sinjalit , ^[1] modulimin e amplitudës kuadratike dhe teorinë e informacionit .

Përkufizimi

Një ndryshore e rastit komplekse $Z$ në hapësirën e probabilitetit $(\Omega ,{\mathcal {F}},P)$ është një funksion $Z\colon \Omega \rightarrow \mathbb {C}$ i tillë që edhe pjesa reale e saj $\Re {(Z)}$ dhe pjesa e saj imagjinare $\Im {(Z)}$ janë ndryshore të rastit reale në $(\Omega ,{\mathcal {F}},P)$ .

Shembuj

Shembull i thjeshtë

Konsideroni një ndryshore të rastit që mund të marrë vetëm tre vlerat komplekse $1+i,1-i,2$ me probabilitete të përcaktuara në tabelë. Ky është një shembull i thjeshtë i një ndryshoreje të rastit komplekse.

Probabiliteti $P(z)$	Vlera $z$
${\frac {1}{4}}$	$1+i$
${\frac {1}{4}}$	$1-i$
${\frac {1}{2}}$	$2$

Pritshmëria e kësaj ndryshoreje të rastit mund të llogaritet thjesht: $\operatorname {E} [Z]={\frac {1}{4}}(1+i)+{\frac {1}{4}}(1-i)+{\frac {1}{2}}2={\frac {3}{2}}.$

Shpërndarja uniforme

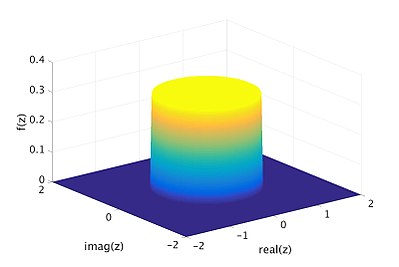
Një shembull tjetër i një ndryshoreje komplekse të rastit është shpërndarja uniforme mbi rrethin njësi të mbushur, dmth $\{z\in \mathbb {C} \mid |z|\leq 1\}$ . Kjo ndryshore e rastit është një shembull i një ndryshoreje komplekse të rastit për të cilën është përcaktuar funksioni i densitetit të probabilitetit . Funksioni i dendësisë është paraqitur si disku i verdhë dhe baza blu e errët në figurën e mëposhtme.

Shpërndarja normale komplekse

Ndryshoret komplekse normale të rastit shpesh hasen në zbatime të shumta. Ato janë një përgjithësim i drejtpërdrejtë i ndryshoreve të rastit normale. Grafiku i mëposhtëm tregon një shembull të shpërndarjes së një ndryshoreje të tillë.

Funksioni kumulativ i shpërndarjes

Përgjithësimi i funksionit të shpërndarjes mbledhëse nga ndryshoret e rastit reale në ato komplekse nuk është i qartë sepse shprehjet e formës $P(Z\leq 1+3i)$ nuk kanë kuptim. Megjithatë shprehjet e formës $P(\Re {(Z)}\leq 1,\Im {(Z)}\leq 3)$ kanë kuptim. Prandaj, ne përcaktojmë shpërndarjen kumulative $F_{Z}:\mathbb {C} \to [0,1]$ të një ndryshoreje komplekse të rastit nëpërmjet shpërndarjes së përbashkët të pjesëve të tyre reale dhe imagjinare:

$F_{Z}(z)=F_{\Re {(Z)},\Im {(Z)}}(\Re {(z)},\Im {(z)})=P(\Re {(Z)}\leq \Re {(z)},\Im {(Z)}\leq \Im {(z)})$ Stampa:Equation box 1

Funksioni i dendësisë së probabilitetit

Funksioni i dendësisë së probabilitetit të një ndryshoreje komplekse të rastit përcaktohet si $f_{Z}(z)=f_{\Re {(Z)},\Im {(Z)}}(\Re {(z)},\Im {(z)})$ , pra vlera e funksionit të dendësisë në një pikë $z\in \mathbb {C}$ është përcaktuar të jetë e barabartë me vlerën e dendësisë së përbashkët të pjesëve reale dhe imagjinare të ndryshores së rastit të vlerësuar në pikën $(\Re {(z)},\Im {(z)})$ .

Një përkufizim i njëvlershëm jepet nga $f_{Z}(z)={\frac {\partial ^{2}}{\partial x\partial y}}P(\Re {(Z)}\leq x,\Im {(Z)}\leq y)$ ku $x=\Re {(z)}$ dhe $y=\Im {(z)}$ .

Si në rastin real, funksioni i dendësisë mund të mos ekzistojë.

Pritja matematike

Pritja matematike e një ndryshoreje komplekse të rastit përcaktohet bazuar në përkufizimin e pritshmërisë së një ndryshoreje të rastit reale: ^[2] ^{:p. 112}

$\operatorname {E} [Z]=\operatorname {E} [\Re {(Z)}]+i\operatorname {E} [\Im {(Z)}]$ Stampa:Equation box 1Vini re se pritja matematike e një ndryshoreje të rastit komplekse nuk ekziston nëse $\operatorname {E} [\Re {(Z)}]$ ose $\operatorname {E} [\Im {(Z)}]$ nuk ekziston.

Nëse ndryshorja e rastit komplekse $Z$ ka një funksion të dendësisë së probabilitetit $f_{Z}(z)$ , atëherë pritja matematike jepet nga $\operatorname {E} [Z]=\iint _{\mathbb {C} }z\cdot f_{Z}(z)\,dx\,dy$ .

Nëse ndryshorja e rastësishme komplekse $Z$ ka një funksion të masës së probabilitetit $p_{Z}(z)$ , atëherë pritja matematike jepet nga $\operatorname {E} [Z]=\sum _{z\in \mathbb {Z} }z\cdot p_{Z}(z)$ .

Kurdoherë që ekziston pritja e një ndryshoreje komplekse të rastit, duke marrë pritshmërinë dhe konjugimin kompleks :

{\overline {\operatorname {E} [Z]}}=\operatorname {E} [{\overline {Z}}].

Veprimi i pritjes matematike $\operatorname {E} [\cdot ]$ është linear në kuptimin që

\operatorname {E} [aZ+bW]=a\operatorname {E} [Z]+b\operatorname {E} [W]

për çdo koeficient kompleks $a,b$ edhe nëse $Z$ dhe $W$ nuk janë të pavarura .

Varianca

Varianca përcaktohet në terma të katrorëve absolutë si: ^[2] :

$\operatorname {K} _{ZZ}=\operatorname {Var} [Z]=\operatorname {E} \left[\left|Z-\operatorname {E} [Z]\right|^{2}\right]=\operatorname {E} [|Z|^{2}]-\left|\operatorname {E} [Z]\right|^{2}$ Stampa:Equation box 1Varianca është gjithmonë një numër real jonegativ. Është e barabartë me shumën e variancave të pjesës reale dhe imagjinare të ndryshores komplekse të rastit:

\operatorname {Var} [Z]=\operatorname {Var} [\Re {(Z)}]+\operatorname {Var} [\Im {(Z)}].

Varianca e një kombinimi linear të ndryshoreve komplekse të rastit mund të llogaritet duke përdorur formulën e mëposhtme:

\operatorname {Var} \left[\sum _{k=1}^{N}a_{k}Z_{k}\right]=\sum _{i=1}^{N}\sum _{j=1}^{N}a_{i}{\overline {a_{j}}}\operatorname {Cov} [Z_{i},Z_{j}].

Mosbarazimi Koshi-Shvarc

Mosbarazimi Koshi-Shvarc për ndryshoret e rastit komplekse, i cili mund të nxirret duke përdorur mosbarazimin e trekëndëshit dhe mosbarazimin e Holderit, është

\left|\operatorname {E} \left[Z{\overline {W}}\right]\right|^{2}\leq \left|\operatorname {E} \left[\left|Z{\overline {W}}\right|\right]\right|^{2}\leq \operatorname {E} \left[|Z|^{2}\right]\operatorname {E} \left[|W|^{2}\right]

.

Funksioni karakteristik

Funksioni karakteristik i një ndryshoreje të rastit komplekse është një funksion $\mathbb {C} \to \mathbb {C}$ përcaktuar nga

\varphi _{Z}(\omega )=\operatorname {E} \left[e^{i\Re {({\overline {\omega }}Z)}}\right]=\operatorname {E} \left[e^{i(\Re {(\omega )}\Re {(Z)}+\Im {(\omega )}\Im {(Z)})}\right].

^ Lapidoth, A. (2009). A Foundation in Digital Communication. Cambridge University Press. ISBN 9780521193955. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!)
^ ^a ^b Park,Kun Il (2018). Fundamentals of Probability and Stochastic Processes with Applications to Communications. Springer. ISBN 978-3-319-68074-3. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!) Gabim referencash: Invalid <ref> tag; name "KunIlPark" defined multiple times with different content

[1] Lapidoth, A. (2009). A Foundation in Digital Communication. Cambridge University Press. ISBN 9780521193955. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!)

[KunIlPark-2] Park,Kun Il (2018). Fundamentals of Probability and Stochastic Processes with Applications to Communications. Springer. ISBN 978-3-319-68074-3. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!) Gabim referencash: Invalid <ref> tag; name "KunIlPark" defined multiple times with different content

[1]

[2]