Shpërndarja hipergjeometrike negative

Hipergjeometrike negative

Probability mass function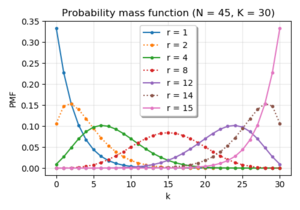
Cumulative distribution function
Parametrat	$N\in \left\{0,1,2,\dots \right\}$ - numri total i elementeve $K\in \left\{0,1,2,\dots ,N\right\}$ - numri total i elementeve 'sukses' $r\in \left\{0,1,2,\dots ,N-K\right\}$ - numri i dështimeve kur eksperimenti ndalohet
Mbështetës	$k\in \left\{0,\,\dots ,\,K\right\}$ - numri i sukseseve kur eksperimenti ndalohet.
FMGJ	${\frac {{{k+r-1} \choose {k}}{{N-r-k} \choose {K-k}}}{N \choose K}}$
Vlera e pritur	$r{\frac {K}{N-K+1}}$
Varianca	$r{\frac {(N+1)K}{(N-K+1)(N-K+2)}}[1-{\frac {r}{N-K+1}}]$

Në teorinë e probabilitetit dhe statistikë, shpërndarja hipergjeometrike negative përshkruan probabilitetet për marrjen e mostrave nga një popullsi e fundme pa zëvendësim, në të cilën çdo popullim mund të klasifikohet në dy kategori ndërsjellazi përjashtuese si Sukses/Dështim ose i Punësuar/I papunësuar. Ndërsa zgjedhjet e rastësishme bëhen nga popullsia, çdo tërheqje e mëpasshme zvogëlon popullsinë duke bërë që probabiliteti i suksesit të ndryshojë me çdo tërheqje. Ndryshe nga shpërndarja standarde hipergjeometrike, e cila përshkruan numrin e sukseseve në një madhësi fikse kampioni, në shpërndarjen hipergjeometrike negative, popullimet nxirren deri sa janë gjetur $r$ dështime dhe shpërndarja përshkruan probabilitetin e gjetjes $k$ sukseseve në një popullim të tillë. Me fjalë të tjera, shpërndarja negative hipergjeometrike përshkruan gjasat e $k$ sukseseve në një popullim me saktësisht $r$ dështime.

Përkufizimi

Ka $N$ elemente, nga të cilat $K$ përkufizohen si "suksese" dhe pjesa tjetër janë "dështime".

Elementet vizatohen njëri pas tjetrit, pa zëvendësime, derisa hasen $r$ dështime. Pastaj, zgjedhja ndalon dhe numri i $k$ sukseseve numërohet. Shpërndarja negative hipergjeometrike, $NHG_{N,K,r}(k)$ është shpërndarja diskrete e kësaj $k$ .

Shpërndarja hipergjeometrike negative është një rast i veçantë i shpërndarjes beta-binomiale me parametra $\alpha =r$ dhe $\beta =N-K-r+1$ të dy duke qenë numra të plotë (dhe $n=K$ ).

Rezultati kërkon që ne të vëzhgojmë $k$ suksese në $(k+r-1)$ tërheqje dhe copëzat $(k+r){\text{-th}}$ duhet të jenë dështime. Probabiliteti i të parës mund të gjendet me zbatimin e drejtpërdrejtë të shpërndarjes hipergjeometrike $(HG_{N,K,k+r-1}(k))$ dhe probabiliteti i kësaj të fundit është thjesht numri i dështimeve të mbetura $(=N-K-(r-1))$ pjesëtuar me madhësinë e popullsisë së mbetur $(=N-(k+r-1)$ . Probabiliteti për të pasur saktësisht $k$ suksese deri në dështimin $r{\text{-të}}$ (dmth. tërheqja ndalon sapo popullimi të përfshijë numrin e paracaktuar të $r$ dështimeve) atëherë është prodhimi i këtyre dy probabiliteteve:

${\frac {{\binom {K}{k}}{\binom {N-K}{k+r-1-k}}}{\binom {N}{k+r-1}}}\cdot {\frac {N-K-(r-1)}{N-(k+r-1)}}={\frac {{{k+r-1} \choose {k}}{{N-r-k} \choose {K-k}}}{N \choose K}}.$

Prandaj, një ndryshore e rastit $X$ ndjek shpërndarjen hipergjeometrike negative nëse funksioni i masës së probabilitetit të tij (fmp) jepet nga

$f(k;N,K,r)\equiv \Pr(X=k)={\frac {{{k+r-1} \choose {k}}{{N-r-k} \choose {K-k}}}{N \choose K}}\quad {\text{për }}k=0,1,2,\dotsc ,K$

ku

• $N$ është madhësia e popullsisë,
• $K$ është numri i gjëndjeve të suksesshme në popullatë,
• $r$ është numri i dështimeve,
• $k$ është numri i sukseseve të vërejtura,
• $a \choose b$ është një koeficient binomial

Sipas dizajnit, probabilitetet shumohen në 1. Megjithatë, në rast se duam ta tregojmë në mënyrë eksplicite kemi:

$\sum _{k=0}^{K}\Pr(X=k)=\sum _{k=0}^{K}{\frac {{{k+r-1} \choose {k}}{{N-r-k} \choose {K-k}}}{N \choose K}}={\frac {1}{N \choose K}}\sum _{k=0}^{K}{{k+r-1} \choose {k}}{{N-r-k} \choose {K-k}}={\frac {1}{N \choose K}}{N \choose K}=1,$

ku kemi përdorur faktin se,

${\begin{aligned}\sum _{j=0}^{k}{\binom {j+m}{j}}{\binom {n-m-j}{k-j}}&=\sum _{j=0}^{k}(-1)^{j}{\binom {-m-1}{j}}(-1)^{k-j}{\binom {m+1+k-n-2}{k-j}}\\&=(-1)^{k}{\binom {k-n-2}{k}}=(-1)^{k}{\binom {k-(n+1)-1}{k}}={\binom {n+1}{k}},\end{aligned}}$

i cili mund të nxirret duke përdorur identitetin binomial, ${{n \choose k}=(-1)^{k}{k-n-1 \choose k}}$ dhe identiteti Chu-Vandermonde, $\sum _{j=0}^{k}{\binom {m}{j}}{\binom {n-m}{k-j}}={\binom {n}{k}}$, i cili vlen për çdo vlerë komplekse $m$ dhe $n$ dhe çdo numër i plotë jo negativ $k$ .

Pritja matematike

Gjatë numërimit të numrit $k$ të sukseseve përpara $r$ dështimeve, numri i pritshëm i sukseseve është ${\frac {rK}{N-K+1}}$ dhe mund të nxirret si më poshtë.

${\begin{aligned}E[X]&=\sum _{k=0}^{K}k\Pr(X=k)=\sum _{k=0}^{K}k{\frac {{{k+r-1} \choose {k}}{{N-r-k} \choose {K-k}}}{N \choose K}}={\frac {r}{N \choose K}}\left[\sum _{k=0}^{K}{\frac {(k+r)}{r}}{{k+r-1} \choose {r-1}}{{N-r-k} \choose {K-k}}\right]-r\\&={\frac {r}{N \choose K}}\left[\sum _{k=0}^{K}{{k+r} \choose {r}}{{N-r-k} \choose {K-k}}\right]-r={\frac {r}{N \choose K}}\left[\sum _{k=0}^{K}{{k+r} \choose {k}}{{N-r-k} \choose {K-k}}\right]-r\\&={\frac {r}{N \choose K}}\left[{{N+1} \choose K}\right]-r={\frac {rK}{N-K+1}},\end{aligned}}$

ku kemi përdorur marrëdhënien $\sum _{j=0}^{k}{\binom {j+m}{j}}{\binom {n-m-j}{k-j}}={\binom {n+1}{k}}$, që kemi nxjerrë më lart për të treguar se shpërndarja negative hipergjeometrike ishte normalizuar siç duhet.

Varianca

Varianca mund të nxirret nga llogaritja e mëposhtme.

${\begin{aligned}E[X^{2}]&=\sum _{k=0}^{K}k^{2}\Pr(X=k)=\left[\sum _{k=0}^{K}(k+r)(k+r+1)\Pr(X=k)\right]-(2r+1)E[X]-r^{2}-r\\&={\frac {r(r+1)}{N \choose K}}\left[\sum _{k=0}^{K}{{k+r+1} \choose {r+1}}{{N+1-(r+1)-k} \choose {K-k}}\right]-(2r+1)E[X]-r^{2}-r\\&={\frac {r(r+1)}{N \choose K}}\left[{{N+2} \choose K}\right]-(2r+1)E[X]-r^{2}-r={\frac {rK(N-r+Kr+1)}{(N-K+1)(N-K+2)}}\end{aligned}}$

Atëherë varianca është ${\textrm {Var}}[X]=E[X^{2}]-\left(E[X]\right)^{2}={\frac {rK(N+1)(N-K-r+1)}{(N-K+1)^{2}(N-K+2)}}$

Shpërndarjet e ndërlidhura

Nëse tërheqja ndalet pas një numri konstant $n$ tërheqjesh (pavarësisht nga numri i dështimeve), atëherë numri i sukseseve ndjek shpërndarjen hipergjeometrike, $HG_{N,K,n}(k)$ . Të dy funksionet janë të lidhura në mënyrën e mëposhtme:

$NHG_{N,K,r}(k)=1-HG_{N,N-K,k+r}(r-1)$

Shpërndarja negative-hipergjeometrike (si shpërndarja hipergjeometrike) merret me tërheqjet pa zëvendësim, kështu që probabiliteti i suksesit është i ndryshëm në çdo barazim. Në të kundërt, shpërndarja binomiale negative (si shpërndarja binomiale) merret me tërheqjet me zëvendësim, në mënyrë që probabiliteti i suksesit të jetë i njëjtë dhe provat të jenë të pavarura. Tabela e mëposhtme përmbledh katër shpërndarjet që lidhen me tërheqjen e sendeve:

	Me zëvendësime	Asnjë zëvendësim
# i sukseseve në # konstant të tërheqjeve	shpërndarja binomiale	shpërndarja hipergjeometrike
# i sukseseve në # konstant të dështimeve	shpërndarje binomiale negative	shpërndarje hipergjeometrike negative

Disa autorë përcaktojnë shpërndarjen negative hipergjeometrike si numrin e tërheqjeve të nevojshme për të marrë $r$ dështime. Le të jetë $Y$ shënimi këtë numër. Atëherë është e qartë se $Y=X+r$ ku Nuk e kuptoj (MathML: Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:6011/sq.wikipedia.org/v1/":): {\displaystyle X} është siç është përcaktuar më sipër. Prandaj FMP $Pr(Y=y)={\binom {y-1}{r-1}}{\frac {\binom {N-y}{N-K-r}}{\binom {N}{N-K}}}$ . Nëse e shënojmë numrin e dështimeve $N-K$ me $M$ do të thotë që kemi $Pr(Y=y)={\binom {y-1}{r-1}}{\frac {\binom {N-y}{M-r}}{\binom {N}{M}}}$ . Bashkësia e përcaktimit e $Y$ është bashkësia $\{r,r+1,\dots ,N-M+r\}$ . Është e qartë se $E[Y]=E[X]+r={\frac {r(N+1)}{M+1}}$ dhe ajo ${\textrm {Var}}[X]={\textrm {Var}}[Y]$ .