Grafiku i një funksioni

Në matematikë, grafiku i një funksioni është bashkësia e çifteve të renditura , ku Në rastin e zakonshëm ku dhe janë numra realë, këto çifte janë koordinata karteziane të pikave në një rrafsh dhe shpesh formojnë një kurbë . Paraqitja grafike e grafikut të një funksioni njihet edhe si grafik .
Në rastin e funksioneve të dy ndryshoreve - domethënë funksione, bashkësia e përcaktimit të së cilave përbëhet nga çifte –, grafiku zakonisht i referohet grupit të treshave të renditura ku . Ky është një nëngrup i hapësirës tre-dimensionale ; për një funksion të vazhdueshëm me vlera reale të dy ndryshoreve reale, grafiku i tij formon një sipërfaqe, e cila mund të vizualizohet si një grafik sipërfaqësor .
Në shkencë, inxhinieri, teknologji, financa dhe fusha të tjera, grafikët janë mjete që përdoren për shumë qëllime. Në rastin më të thjeshtë, një ndryshore vizatohet si funksion i një tjetre, zakonisht duke përdorur boshte drejtkëndore.
Një grafik i një funksioni është një rast i veçantë i një relacioni . Në bazat moderne të matematikës, dhe, zakonisht, në teorinë e bashkësive, një funksion është në të vërtetë i barabartë me grafikun e tij. [1] Megjithatë, shpesh është e dobishme të shihen funksionet si hartëzime, [2] të cilat përbëhen jo vetëm nga lidhja midis hyrjes dhe daljes, por gjithashtu se cila bashkësi është bashkësia e përcaktimit dhe cila bashkësi është bashkësia e shëmbëllimeve . Për shembull, të themi se një funksion është onto ( syrjektiv ) ose jo, duhet të merret parasysh bashkësia e shëmbëllimeve. Grafiku i një funksioni në vetvete nuk e përcakton B e shëmbëllimeve. Është e zakonshme [3] të përdoren të dy termat funksion dhe grafik i një funksioni pasi edhe nëse konsiderohen i njëjti objekt, ato tregojnë shikimin e tij nga një këndvështrim tjetër.
Përkufizimi
[Redakto | Redakto nëpërmjet kodit]Jepet një funksion nga një bashkësia X ( domeni ) në një bashkësi Y ( kodomeni ), grafiku i funksionit është bashkësia [4] që është një nëngrup i prodhimit kartezian . Në përkufizimin e një funksioni në termat e teorisë së bashkësive, është e zakonshme të identifikohet një funksion me grafikun e tij, megjithëse, zyrtarisht, një funksion formohet nga trefishi i përbërë nga domeni i tij, kodomani dhe grafiku i tij.
Shembuj
[Redakto | Redakto nëpërmjet kodit]Funksionet e një ndryshoreje
[Redakto | Redakto nëpërmjet kodit]
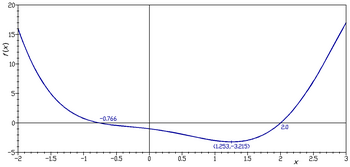
Grafiku i funksionit përcaktuar nga është nënbashkësi e bashkësisë
Grafiku i polinomit kub në drejtëzën reale është
Nëse ky grup paraqitet në një rrafsh kartezian, rezultati është një kurbë (shih figurën).
Funksionet e dy ndryshoreve
[Redakto | Redakto nëpërmjet kodit]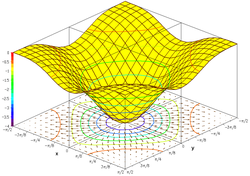
Grafiku i funksionit trigonometrik është
Nëse ky grup paraqitet në një sistem koordinativ tredimensional kartezian, rezultati është një sipërfaqe (shih figurën).
- ^ Charles C Pinter (2014). A Book of Set Theory. Dover Publications. fq. 49. ISBN 978-0-486-79549-2.
{{cite book}}: Mungon ose është bosh parametri|language=(Ndihmë!) - ^ T. M. Apostol (1981). Mathematical Analysis. Addison-Wesley. fq. 35.
{{cite book}}: Mungon ose është bosh parametri|language=(Ndihmë!) - ^ P. R. Halmos (1982). A Hilbert Space Problem Book. Springer-Verlag. fq. 31. ISBN 0-387-90685-1.
{{cite book}}: Mungon ose është bosh parametri|language=(Ndihmë!) - ^ D. S. Bridges (1991). Foundations of Real and Abstract Analysis. Springer. fq. 285. ISBN 0-387-98239-6.
{{cite book}}: Mungon ose është bosh parametri|language=(Ndihmë!)






















