Shpërndarja trekëndore

Trekëndor

Cumulative distribution function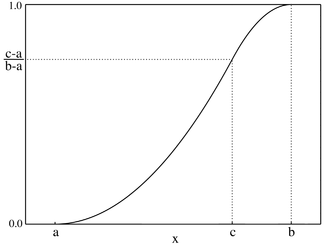
Parametrat	$a:~a\in (-\infty ,\infty )$ $b:~a<b\,$ $c:~a\leq c\leq b\,$
Mbështetës	$a\leq x\leq b\!$
	${\begin{cases}0&{\text{për }}x<a,\\{\frac {2(x-a)}{(b-a)(c-a)}}&{\text{për }}a\leq x<c,\\[4pt]{\frac {2}{b-a}}&{\text{për }}x=c,\\[4pt]{\frac {2(b-x)}{(b-a)(b-c)}}&{\text{për }}c<x\leq b,\\[4pt]0&{\text{për }}b<x.\end{cases}}$
FGSH	${\begin{cases}0&{\text{për }}x\leq a,\\[2pt]{\frac {(x-a)^{2}}{(b-a)(c-a)}}&{\text{për }}a<x\leq c,\\[4pt]1-{\frac {(b-x)^{2}}{(b-a)(b-c)}}&{\text{për }}c<x<b,\\[4pt]1&{\text{për }}b\leq x.\end{cases}}$
Vlera e pritur	${\frac {a+b+c}{3}}$
Mediana	${\begin{cases}a+{\sqrt {\frac {(b-a)(c-a)}{2}}}&{\text{për }}c\geq {\frac {a+b}{2}},\\[6pt]b-{\sqrt {\frac {(b-a)(b-c)}{2}}}&{\text{për }}c\leq {\frac {a+b}{2}}.\end{cases}}$
Moda	$c\,$
	${\frac {a^{2}+b^{2}+c^{2}-ab-ac-bc}{18}}$
Shtrirja	${\frac {{\sqrt {2}}(a\!+\!b\!-\!2c)(2a\!-\!b\!-\!c)(a\!-\!2b\!+\!c)}{5(a^{2}\!+\!b^{2}\!+\!c^{2}\!-\!ab\!-\!ac\!-\!bc)^{\frac {3}{2}}}}$
Kurtoza e tepërt	$-{\frac {3}{5}}$
Entropia	${\frac {1}{2}}+\ln \left({\frac {b-a}{2}}\right)$
FGJM	$2{\frac {(b\!-\!c)e^{at}\!-\!(b\!-\!a)e^{ct}\!+\!(c\!-\!a)e^{bt}}{(b-a)(c-a)(b-c)t^{2}}}$
FK	$-2{\frac {(b\!-\!c)e^{iat}\!-\!(b\!-\!a)e^{ict}\!+\!(c\!-\!a)e^{ibt}}{(b-a)(c-a)(b-c)t^{2}}}$

Në teorinë e probabilitetit dhe statistikë, shpërndarja trekëndore është një shpërndarje e vazhdueshme me kufirin e poshtëm a, kufirin e sipërm b dhe modën c, ku a < b dhe a ≤ c ≤ b .

Raste të veçanta

Moda në një kufi

Shpërndarja thjeshtohet kur c = a ose c = b . Për shembull, nëse a = 0, b = 1 dhe c = 1, atëherë PDF dhe CDF bëhen:

$\left.{\begin{array}{rl}f(x)&=2x\\[8pt]F(x)&=x^{2}\end{array}}\right\}{\text{ për }}0\leq x\leq 1$

${\begin{aligned}\operatorname {E} (X)&={\frac {2}{3}}\\[8pt]\operatorname {Var} (X)&={\frac {1}{18}}\end{aligned}}$

Shpërndarja e diferencës absolute të dy variablave standarde uniforme

Kjo shpërndarje për një a = 0, b = 1 dhe c = 0 është shpërndarja e X = | X ₁ − X ₂ |, ku X ₁, X ₂ janë dy ndryshore rasti të pavarura me shpërndarje standarde uniforme .

${\begin{aligned}f(x)&=2-2x{\text{ për }}0\leq x<1\\[6pt]F(x)&=2x-x^{2}{\text{ për }}0\leq x<1\\[6pt]E(X)&={\frac {1}{3}}\\[6pt]\operatorname {Var} (X)&={\frac {1}{18}}\end{aligned}}$

Shpërndarja trekëndore simetrike

Rasti simetrik lind kur c = ( a + b ) / 2. Në këtë rast, një formë alternative e funksionit të shpërndarjes është:

${\begin{aligned}f(x)&={\frac {(b-c)-|c-x|}{(b-c)^{2}}}\\[6pt]\end{aligned}}$

Gjenerimi i variateve të rastit trekëndësh të shpërndara

Jepet një variat i rastit U i nxjerrë nga shpërndarja uniforme në intervalin (0, 1), më pas variati

$X={\begin{cases}a+{\sqrt {U(b-a)(c-a)}}&{\text{ për }}0<U<F(c)\\&\\b-{\sqrt {(1-U)(b-a)(b-c)}}&{\text{ për }}F(c)\leq U<1\end{cases}}$

ku $F(c)=(c-a)/(b-a)$, ka shpërndarje trekëndore me parametra $a,b$ dhe $c$ . Kjo mund të merret nga funksioni i shpërndarjes mbledhëse.

Përdorimi i shpërndarjes

Shpërndarja trekëndore zakonisht përdoret si një përshkrim subjektiv i një popullate për të cilën ka vetëm të dhëna të kufizuara të mostrës, dhe veçanërisht në rastet kur lidhja midis variablave është e njohur, por të dhënat janë të pakta (ndoshta për shkak të kostos së lartë të grumbullimit). Ai bazohet në një njohuri të minimumit dhe maksimumit dhe një "supozim të frymëzuar" për vlerën modale. Për këto arsye, shpërndarja e trekëndëshit është quajtur shpërndarje e "mungesës së njohurisë".

Simulimet e biznesit

Prandaj, shpërndarja trekëndore përdoret shpesh në vendimmarrjen e biznesit, veçanërisht në simulime . Në përgjithësi, kur nuk dihet shumë për shpërndarjen e një rezultati (të themi, vetëm vlerat e tij më të vogla dhe më të mëdha), është e mundur të përdoret shpërndarja uniforme . Por nëse dihet edhe rezultati më i mundshëm, atëherë rezultati mund të simulohet nga një shpërndarje trekëndore. Shih për shembull nën financat e korporatave .

Menaxhimi i projektit

Shpërndarja trekëndore, së bashku me shpërndarjen PERT, përdoret gjithashtu gjerësisht në menaxhimin e projekteve (si një hyrje në PERT dhe rrjedhimisht metodën e rrugës kritike (CPM)) për të modeluar ngjarjet që ndodhin brenda një intervali të përcaktuar nga një vlerë minimale dhe maksimale.

Akumulimi i audios

Shpërndarja trekëndore simetrike përdoret zakonisht në zhurmën e zërit, ku quhet TPDF (funksioni i densitetit të probabilitetit trekëndor).

Formimi i rrezeve

Shpërndarja trekëndore gjen zbatim në formimin e rrezeve dhe sintezën e modelit.