Prerjet konike

Preje konike në përgjithësi është lakorja që fitohet kur një sipërfaqja konike rrethore pritet me një rrafsh. Prerjet konike janë studjuar sistematikisht nga matematikani i Greqisë antike Apolloni i Pergës.

Llojet e prerjeve konike

Llojet e prerjeve konike

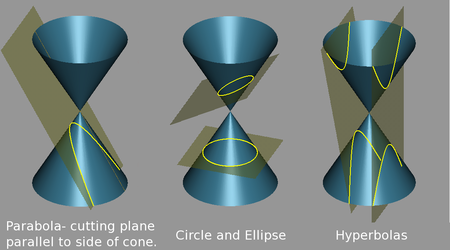
Në përgjithësi ekzistojnë 3 lloje të prerjeve konike dhe ato janë hiperbola, elipsa, dhe parabola. Rrethi konsiderohet si nënlloj i elipsës.Rrethi dhe elipsa janë lakore të mbyllura. Rrethi fitohet kur sipërfaqja konike prittet me një rrafsh i cili e pret boshtin dhe gjeneratrisën e sipërfaqes konike rrethore. Nëse sipërfaqja konike pritet me një rrafsh i cili është paralel me gjeneratrisën e saj atëherë fitohet parabola dhe nëse sipërfaqja konike pritet me një rrafsh i cili është paralel me boshtin e saj atëherë si preje konike fitohet hiperbola.

Prerjet konike në gjeometrinë analitike

Gjeometria analitike është degë e matematikës e cila e studjon gjeometrinë me metoda algjebrike. Në një sistem koordinativ kënddrejt grafiku i një funksioni kuadratik me dy ndryshore paraqet një prerje konike. Forma e përgjithshme e barazimit kuadratik me dy ndryshore është

$Ax^2 + Bxy + Cy^2 +Dx + Ey + F = 0$ ku koeficientët $A$, $B$, dhe $C$, njëkohësisht nuk janë të barabartë me 0.

Atëherë kemi:

• Nëse $B^2 - 4AC < 0$, barazimi paraqet një elipsë
• Nëse $A = C$ dhe $B = 0$, atëherë kemi rreth;
• Nëse $B^2 - 4AC = 0$, barazimi paraqet një parabollë;
• Nëse $B^2 - 4AC > 0$, atëherë kemi hiperbolë;

Duke transformuar koordinatat barazimet mund të shëndrrohen në formë kanonike:

• Rrethi: $x^2+y^2=r^2$
• Elipsa: ${x^2\over a^2}+{y^2\over b^2}=1$, ${x^2\over b^2}+{y^2\over a^2}=1$
• Parabola: $y^2=4ax$, $x^2=4ay$
• Hiperbola: ${x^2\over a^2}-{y^2\over b^2}=1$, ${x^2\over a^2}-{y^2\over b^2}=-1$

Format e tilla janë simetrike në lidhje boshtin x ndërsa për rrethin elipsën dhe hiperbolën edhe në lidhje me boshtin y.

Zbatimet

Prerjet konike janë lakore të lëmuara d.m.th ata nuk kanë thyerje apo pika infleksioni prandaj kanë zbatime në aerodinamikë në fizikë trajektorja e një pike materiale gjatë hedhjes në rafshin e tokës është parabollë. Në astronomi , orbita e dy objekteve masive bashkëvepron në pajtim me ligjin gravitacional universal të Njutonit, kjo orbitë është prerje konike nëse qendra e rëndesës është jashtë tyre. Në gjeometrinë projektive, prerjet konike në rrafshin projektiv janë ekuvalente njëri me tjetrin si transformime projektive.

Lidhje të jashtme

• Derivations of Conic Sections at Convergence
• Conic sections at Special plane curves.
• Determinants and Conic Section Curves
• Occurrence of the conics. Conics in nature and elsewhere.
• Conics.
• Conic Sections
• Xah Lee

Conic sections