Në teorinë e probabilitetit dhe statistikë , shpërndarja eksponenciale ose shpërndarja eksponenciale negative është shpërndarja e probabilitetit të kohës ndërmjet ngjarjeve në një proces pikësor Poisson, dmth, një proces në të cilin ngjarjet ndodhin vazhdimisht dhe në mënyrë të pavarur me një normë mesatare konstante. Është një rast i veçantë i shpërndarjes gama . Ai është analogu i vazhdueshëm i shpërndarjes gjeometrike dhe ka vetinë kryesore të të qenit pa memorie . Përveç përdorimit për analizën e proceseve pikësore Poisson, ai haset në kontekste të tjera të ndryshme.
Shpërndarja eksponenciale nuk është e njëjtë me klasën e familjeve eksponenciale të shpërndarjeve. Kjo është një klasë e madhe shpërndarjesh probabiliteti që përfshin shpërndarjen eksponenciale si një nga anëtarët e saj, por gjithashtu përfshin shumë shpërndarje të tjera, si shpërndarjet normale , binomiale , gama dhe Poisson .
Funksioni i dendësisë së probabilitetit (fdp) i një shpërndarjeje eksponenciale është
f
(
x
;
λ
)
=
{
λ
e
−
λ
x
x
≥
0
,
0
x
<
0.
{\displaystyle f(x;\lambda )={\begin{cases}\lambda e^{-\lambda x}&x\geq 0,\\0&x<0.\end{cases}}}
Këtu λ > 0 është parametri i shpërndarjes, i quajtur shpesh parametri i shkallës . Shpërndarja është e përcaktuar në intervalin
[
0
,
∞
)
{\displaystyle [0,\infty )}
ndryshore e rastit
X
{\displaystyle X}
X
∼
Exp
(
λ
)
{\displaystyle X\sim \operatorname {Exp} (\lambda )}
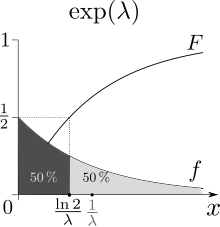
Funksioni i mbledhës i shpërndarjes jepet nga
F
(
x
;
λ
)
=
{
1
−
e
−
λ
x
x
≥
0
,
0
x
<
0.
{\displaystyle F(x;\lambda )={\begin{cases}1-e^{-\lambda x}&x\geq 0,\\0&x<0.\end{cases}}}
Shpërndarja eksponenciale nganjëherë parametrizohet në termat e parametrit të shkallës
β
=
1
/
λ
{\displaystyle \beta =1/\lambda }
f
(
x
;
β
)
=
{
1
β
e
−
x
/
β
x
≥
0
,
0
x
<
0.
F
(
x
;
β
)
=
{
1
−
e
−
x
/
β
x
≥
0
,
0
x
<
0.
{\displaystyle f(x;\beta )={\begin{cases}{\frac {1}{\beta }}e^{-x/\beta }&x\geq 0,\\0&x<0.\end{cases}}\qquad \qquad F(x;\beta )={\begin{cases}1-e^{-x/\beta }&x\geq 0,\\0&x<0.\end{cases}}}
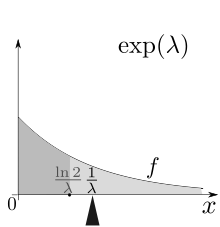
Mesatarja është qendra e masës së probabilitetit, domethënë momenti i parë . Mesorja është paraimazhi F −1 (1/2). Vlera mesatare ose pritja matematike e një ndryshoreje rasti
X
{\displaystyle X}
λ
{\displaystyle \lambda }
E
[
X
]
=
1
λ
.
{\displaystyle \operatorname {E} [X]={\frac {1}{\lambda }}.}
Varianca e
X
{\displaystyle X}
Var
[
X
]
=
1
λ
2
,
{\displaystyle \operatorname {Var} [X]={\frac {1}{\lambda ^{2}}},}
shmangia standarde është e barabartë me mesataren.
Momentet e
X
{\displaystyle X}
n
∈
N
{\displaystyle n\in \mathbb {N} }
E
[
X
n
]
=
n
!
λ
n
.
{\displaystyle \operatorname {E} \left[X^{n}\right]={\frac {n!}{\lambda ^{n}}}.}
X
{\displaystyle X}
n
∈
N
{\displaystyle n\in \mathbb {N} }
μ
n
=
!
n
λ
n
=
n
!
λ
n
∑
k
=
0
n
(
−
1
)
k
k
!
.
{\displaystyle \mu _{n}={\frac {!n}{\lambda ^{n}}}={\frac {n!}{\lambda ^{n}}}\sum _{k=0}^{n}{\frac {(-1)^{k}}{k!}}.}
!
n
{\displaystyle !n}
nënfaktoriali i
n
{\displaystyle n}
. Mesorja e
X
{\displaystyle X}
m
[
X
]
=
ln
(
2
)
λ
<
E
[
X
]
,
{\displaystyle \operatorname {m} [X]={\frac {\ln(2)}{\lambda }}<\operatorname {E} [X],}
ln
{\displaystyle \ln }
|
E
[
X
]
−
m
[
X
]
|
=
1
−
ln
(
2
)
λ
<
1
λ
=
σ
[
X
]
,
{\displaystyle \left|\operatorname {E} \left[X\right]-\operatorname {m} \left[X\right]\right|={\frac {1-\ln(2)}{\lambda }}<{\frac {1}{\lambda }}=\operatorname {\sigma } [X],}
Një ndryshore e rastit
T
{\displaystyle T}
Pr
(
T
>
s
+
t
∣
T
>
s
)
=
Pr
(
T
>
t
)
,
∀
s
,
t
≥
0.
{\displaystyle \Pr \left(T>s+t\mid T>s\right)=\Pr(T>t),\qquad \forall s,t\geq 0.}
Pr
(
T
>
s
+
t
∣
T
>
s
)
=
Pr
(
T
>
s
+
t
∩
T
>
s
)
Pr
(
T
>
s
)
=
Pr
(
T
>
s
+
t
)
Pr
(
T
>
s
)
=
e
−
λ
(
s
+
t
)
e
−
λ
s
=
e
−
λ
t
=
Pr
(
T
>
t
)
.
{\displaystyle {\begin{aligned}\Pr \left(T>s+t\mid T>s\right)&={\frac {\Pr \left(T>s+t\cap T>s\right)}{\Pr \left(T>s\right)}}\\[4pt]&={\frac {\Pr \left(T>s+t\right)}{\Pr \left(T>s\right)}}\\[4pt]&={\frac {e^{-\lambda (s+t)}}{e^{-\lambda s}}}\\[4pt]&=e^{-\lambda t}\\[4pt]&=\Pr(T>t).\end{aligned}}}
T
{\displaystyle T}
T
{\displaystyle T}
s , shpërndarja e kohës së mbetur të pritjes është e njëjtë me shpërndarjen origjinale të pakushtëzuar. Për shembull, nëse një ngjarje nuk ka ndodhur pas 30 sekondash, probabiliteti i kushtëzuar që ndodhia do të marrë të paktën 10 sekonda më shumë është i barabartë me probabilitetin e pakushtëzuar të vëzhgimit të ngjarjes më shumë se 10 sekonda pas kohës fillestare.
Shpërndarja eksponenciale dhe shpërndarja gjeometrike janë të vetmet shpërndarje të probabilitetit pa kujtesë .
Funksioni kuantile (funksioni i shpërndarjes mbledhëse të anasjelltë) për
Exp
(
λ
)
{\displaystyle {\text{Exp}}(\lambda )}
F
−
1
(
p
;
λ
)
=
−
ln
(
1
−
p
)
λ
,
0
≤
p
<
1
{\displaystyle F^{-1}(p;\lambda )={\frac {-\ln(1-p)}{\lambda }},\qquad 0\leq p<1}
kuartili i parë:
ln
(
4
/
3
)
/
λ
{\displaystyle \ln(4/3)/\lambda }
mesorja :
ln
(
2
)
/
λ
{\displaystyle \ln(2)/\lambda }
kuartili i tretë:
ln
(
4
)
/
λ
{\displaystyle \ln(4)/\lambda }
Vlera e kushtëzuar në rrezik (CVaR) e njohur gjithashtu si mungesa e pritshme ose superkuantili për
Exp
(
λ
)
{\displaystyle {\text{Exp}}(\lambda )}
[ 1]
q
¯
α
(
X
)
=
1
1
−
α
∫
α
1
q
p
(
X
)
d
p
=
1
(
1
−
α
)
∫
α
1
−
ln
(
1
−
p
)
λ
d
p
=
−
1
λ
(
1
−
α
)
∫
1
−
α
0
−
ln
(
y
)
d
y
=
−
1
λ
(
1
−
α
)
∫
0
1
−
α
ln
(
y
)
d
y
=
−
1
λ
(
1
−
α
)
[
(
1
−
α
)
ln
(
1
−
α
)
−
(
1
−
α
)
]
=
−
ln
(
1
−
α
)
+
1
λ
{\displaystyle {\begin{aligned}{\bar {q}}_{\alpha }(X)&={\frac {1}{1-\alpha }}\int _{\alpha }^{1}q_{p}(X)dp\\&={\frac {1}{(1-\alpha )}}\int _{\alpha }^{1}{\frac {-\ln(1-p)}{\lambda }}dp\\&={\frac {-1}{\lambda (1-\alpha )}}\int _{1-\alpha }^{0}-\ln(y)dy\\&={\frac {-1}{\lambda (1-\alpha )}}\int _{0}^{1-\alpha }\ln(y)dy\\&={\frac {-1}{\lambda (1-\alpha )}}[(1-\alpha )\ln(1-\alpha )-(1-\alpha )]\\&={\frac {-\ln(1-\alpha )+1}{\lambda }}\\\end{aligned}}}
Divergjenca e drejtuar Kullback–Leibler në nats të
e
λ
{\displaystyle e^{\lambda }}
e
λ
0
{\displaystyle e^{\lambda _{0}}}
Δ
(
λ
0
∥
λ
)
=
E
λ
0
(
log
p
λ
0
(
x
)
p
λ
(
x
)
)
=
E
λ
0
(
log
λ
0
e
λ
0
x
λ
e
λ
x
)
=
log
(
λ
0
)
−
log
(
λ
)
−
(
λ
0
−
λ
)
E
λ
0
(
x
)
=
log
(
λ
0
)
−
log
(
λ
)
+
λ
λ
0
−
1.
{\displaystyle {\begin{aligned}\Delta (\lambda _{0}\parallel \lambda )&=\mathbb {E} _{\lambda _{0}}\left(\log {\frac {p_{\lambda _{0}}(x)}{p_{\lambda }(x)}}\right)\\&=\mathbb {E} _{\lambda _{0}}\left(\log {\frac {\lambda _{0}e^{\lambda _{0}x}}{\lambda e^{\lambda x}}}\right)\\&=\log(\lambda _{0})-\log(\lambda )-(\lambda _{0}-\lambda )E_{\lambda _{0}}(x)\\&=\log(\lambda _{0})-\log(\lambda )+{\frac {\lambda }{\lambda _{0}}}-1.\end{aligned}}}
Funksioni i shpërndarjes së probabilitetit (FSHP) i një shume të dy ndryshoreve të rastit të pavarura është ndërthurja e FSHP-ve të secilës . Nëse
X
1
{\displaystyle X_{1}}
X
2
{\displaystyle X_{2}}
λ
1
{\displaystyle \lambda _{1}}
λ
2
,
{\displaystyle \lambda _{2},}
Z
=
X
1
+
X
2
{\displaystyle Z=X_{1}+X_{2}}
f
Z
(
z
)
=
∫
−
∞
∞
f
X
1
(
x
1
)
f
X
2
(
z
−
x
1
)
d
x
1
=
∫
0
z
λ
1
e
−
λ
1
x
1
λ
2
e
−
λ
2
(
z
−
x
1
)
d
x
1
=
λ
1
λ
2
e
−
λ
2
z
∫
0
z
e
(
λ
2
−
λ
1
)
x
1
d
x
1
=
{
λ
1
λ
2
λ
2
−
λ
1
(
e
−
λ
1
z
−
e
−
λ
2
z
)
if
λ
1
≠
λ
2
λ
2
z
e
−
λ
z
if
λ
1
=
λ
2
=
λ
.
{\displaystyle {\begin{aligned}f_{Z}(z)&=\int _{-\infty }^{\infty }f_{X_{1}}(x_{1})f_{X_{2}}(z-x_{1})\,dx_{1}\\&=\int _{0}^{z}\lambda _{1}e^{-\lambda _{1}x_{1}}\lambda _{2}e^{-\lambda _{2}(z-x_{1})}\,dx_{1}\\&=\lambda _{1}\lambda _{2}e^{-\lambda _{2}z}\int _{0}^{z}e^{(\lambda _{2}-\lambda _{1})x_{1}}\,dx_{1}\\&={\begin{cases}{\dfrac {\lambda _{1}\lambda _{2}}{\lambda _{2}-\lambda _{1}}}\left(e^{-\lambda _{1}z}-e^{-\lambda _{2}z}\right)&{\text{ if }}\lambda _{1}\neq \lambda _{2}\\[4pt]\lambda ^{2}ze^{-\lambda z}&{\text{ if }}\lambda _{1}=\lambda _{2}=\lambda .\end{cases}}\end{aligned}}}
Nëse
X
{\displaystyle X}
Laplace(μ, β−1 ) , atëherë
|
X
−
μ
|
∼
Exp
(
β
)
{\displaystyle |X-\mu |\sim \operatorname {Exp} (\beta )}
Nëse
X
{\displaystyle X}
Pareto(1, λ) , atëherë
log
(
X
)
∼
Exp
(
λ
)
{\displaystyle \log(X)\sim \operatorname {Exp} (\lambda )}
Nëse
X
{\displaystyle X}
log
(
1
+
e
−
X
)
∼
Exp
(
θ
)
{\displaystyle \log \left(1+e^{-X}\right)\sim \operatorname {Exp} (\theta )}
Nëse
X
i
∼
U
(
0
,
1
)
{\displaystyle X_{i}\sim U(0,1)}
lim
n
→
∞
n
min
(
X
1
,
…
,
X
n
)
∼
Exp
(
1
)
{\displaystyle \lim _{n\to \infty }n\min \left(X_{1},\ldots ,X_{n}\right)\sim \operatorname {Exp} (1)}
Shpërndarja eksponenciale është një limit i asaj beta :
lim
n
→
∞
n
Beta
(
1
,
n
)
=
Exp
(
1
)
.
{\displaystyle \lim _{n\to \infty }n\operatorname {Beta} (1,n)=\operatorname {Exp} (1).}
Nëse
X
∼
Exp
(
λ
)
{\displaystyle X\sim {\text{Exp}}(\lambda )}
X
i
∼
Exp
(
λ
i
)
{\displaystyle X_{i}\sim {\text{Exp}}(\lambda _{i})}
k
X
∼
Exp
(
λ
k
)
{\displaystyle kX\sim \operatorname {Exp} \left({\frac {\lambda }{k}}\right)}
k
e
X
{\displaystyle ke^{X}}
∼
{\displaystyle \sim }
Pareto
(
k
,
λ
)
{\displaystyle (k,\lambda )}
e
−
X
{\displaystyle e^{-X}}
∼
{\displaystyle \sim }
Beta
(
λ
,
1
)
{\displaystyle \operatorname {Beta} (\lambda ,1)}
e
X
{\displaystyle e^{X}}
PowerLaw
(
k
,
λ
)
{\displaystyle (k,\lambda )}
X
∼
Rayleigh
(
1
2
λ
)
{\displaystyle {\sqrt {X}}\sim \operatorname {Rayleigh} \left({\frac {1}{\sqrt {2\lambda }}}\right)}
X
∼
Weibull
(
1
λ
,
1
)
{\displaystyle X\sim \operatorname {Weibull} \left({\frac {1}{\lambda }},1\right)}
X
2
∼
Weibull
(
1
λ
2
,
1
2
)
{\displaystyle X^{2}\sim \operatorname {Weibull} \left({\frac {1}{\lambda ^{2}}},{\frac {1}{2}}\right)}
μ
−
β
log
(
λ
X
)
∼
Gumbel
(
μ
,
β
)
{\displaystyle \mu -\beta \log(\lambda X)\sim {\text{Gumbel}}(\mu ,\beta )}
⌊
X
⌋
∼
Geometric
(
1
−
e
−
λ
)
{\displaystyle \lfloor X\rfloor \sim \operatorname {Geometric} \left(1-e^{-\lambda }\right)}
shpërndarje gjeometrike në 0,1,2,3,...
⌈
X
⌉
∼
Geometric
(
1
−
e
−
λ
)
{\displaystyle \lceil X\rceil \sim \operatorname {Geometric} \left(1-e^{-\lambda }\right)}
shpërndarje gjeometrike në 1,2,3,4,...Nëse
Y
∼
Erlang
(
n
,
λ
)
{\displaystyle Y\sim {\text{Erlang}}(n,\lambda )}
Y
∼
Γ
(
n
,
1
λ
)
{\displaystyle Y\sim \Gamma \left(n,{\frac {1}{\lambda }}\right)}
X
Y
+
1
∼
Pareto
(
1
,
n
)
{\displaystyle {\frac {X}{Y}}+1\sim \operatorname {Pareto} (1,n)}
λ
1
X
1
−
λ
2
Y
2
∼
{\displaystyle \lambda _{1}X_{1}-\lambda _{2}Y_{2}\sim }
Laplas(0, 1) .Nëse gjithashtu
λ
i
=
λ
{\displaystyle \lambda _{i}=\lambda }
X
1
+
⋯
+
X
k
=
∑
i
X
i
∼
{\displaystyle X_{1}+\cdots +X_{k}=\sum _{i}X_{i}\sim }
Erlang
(
k
,
λ
)
{\displaystyle \operatorname {Erlang} (k,\lambda )}
Gamma
(
k
,
λ
−
1
)
{\displaystyle \operatorname {Gamma} (k,\lambda ^{-1})}
Gamma
(
k
,
λ
)
{\displaystyle \operatorname {Gamma} (k,\lambda )}
[ 2] Nëse
T
=
(
X
1
+
⋯
+
X
n
)
=
∑
i
=
1
n
X
i
{\displaystyle T=(X_{1}+\cdots +X_{n})=\sum _{i=1}^{n}X_{i}}
2
λ
T
∼
χ
2
n
2
{\displaystyle 2\lambda T\sim \chi _{2n}^{2}}
X
i
−
X
j
∼
{\displaystyle X_{i}-X_{j}\sim }
Laplace
(
0
,
λ
−
1
)
{\displaystyle \operatorname {Laplace} (0,\lambda ^{-1})}
Nëse gjithashtu
X
i
{\displaystyle X_{i}}
X
i
X
i
+
X
j
∼
U
(
0
,
1
)
{\displaystyle {\frac {X_{i}}{X_{i}+X_{j}}}\sim \operatorname {U} (0,1)}
Z
=
λ
i
X
i
λ
j
X
j
{\displaystyle Z={\frac {\lambda _{i}X_{i}}{\lambda _{j}X_{j}}}}
f
Z
(
z
)
=
1
(
z
+
1
)
2
{\displaystyle f_{Z}(z)={\frac {1}{(z+1)^{2}}}}
Nëse gjithashtu λ = 1:
μ
−
β
log
(
e
−
X
1
−
e
−
X
)
∼
Logistic
(
μ
,
β
)
{\displaystyle \mu -\beta \log \left({\frac {e^{-X}}{1-e^{-X}}}\right)\sim \operatorname {Logistic} (\mu ,\beta )}
μ
−
β
log
(
X
i
X
j
)
∼
Logistic
(
μ
,
β
)
{\displaystyle \mu -\beta \log \left({\frac {X_{i}}{X_{j}}}\right)\sim \operatorname {Logistic} (\mu ,\beta )}
Më tej , nëse
Y
∼
Γ
(
α
,
β
α
)
{\displaystyle Y\sim \Gamma \left(\alpha ,{\frac {\beta }{\alpha }}\right)}
X
Y
∼
K
(
α
,
β
)
{\displaystyle {\sqrt {XY}}\sim \operatorname {K} (\alpha ,\beta )}
Nëse gjithashtu
λ
=
1
/
2
{\displaystyle \lambda =1/2}
X
∼
χ
2
2
{\displaystyle X\sim \chi _{2}^{2}}
X
{\displaystyle X}
shpërndarje hi katror with 2 shkallë lirie. Kështu:
Exp
(
λ
)
=
1
2
λ
Exp
(
1
2
)
∼
1
2
λ
χ
2
2
⇒
∑
i
=
1
n
Exp
(
λ
)
∼
1
2
λ
χ
2
n
2
{\displaystyle \operatorname {Exp} (\lambda )={\frac {1}{2\lambda }}\operatorname {Exp} \left({\frac {1}{2}}\right)\sim {\frac {1}{2\lambda }}\chi _{2}^{2}\Rightarrow \sum _{i=1}^{n}\operatorname {Exp} (\lambda )\sim {\frac {1}{2\lambda }}\chi _{2n}^{2}}
Nëse
X
∼
Exp
(
1
λ
)
{\displaystyle X\sim \operatorname {Exp} \left({\frac {1}{\lambda }}\right)}
Y
∣
X
{\displaystyle Y\mid X}
Poisson(X ) atëherë
Y
∼
Geometric
(
1
1
+
λ
)
{\displaystyle Y\sim \operatorname {Geometric} \left({\frac {1}{1+\lambda }}\right)}
shpërndarja gjeometrike )
Më poshtë, supozoni se ndryshorja e rastit
X
{\displaystyle X}
λ
{\displaystyle \lambda }
x
1
,
…
,
x
n
{\displaystyle x_{1},\dotsc ,x_{n}}
n
{\displaystyle n}
X
{\displaystyle X}
x
¯
{\displaystyle {\bar {x}}}
Vlerësuesi i përgjasisë maksimale për
λ
{\displaystyle \lambda }
Funksioni i përgjasisë për
λ
{\displaystyle \lambda }
x
=
(
x
1
,
x
2
,
.
.
.
,
x
n
)
{\displaystyle x=(x_{1},x_{2},...,x_{n})}
L
(
λ
)
=
∏
i
=
1
n
λ
exp
(
−
λ
x
i
)
=
λ
n
exp
(
−
λ
∑
i
=
1
n
x
i
)
=
λ
n
exp
(
−
λ
n
x
¯
)
,
{\displaystyle L(\lambda )=\prod _{i=1}^{n}\lambda \exp(-\lambda x_{i})=\lambda ^{n}\exp \left(-\lambda \sum _{i=1}^{n}x_{i}\right)=\lambda ^{n}\exp \left(-\lambda n{\overline {x}}\right),}
x
¯
=
1
n
∑
i
=
1
n
x
i
{\displaystyle {\overline {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}}
Derivati i logaritmit të funksionit të përgjasisë është:
d
d
λ
ln
L
(
λ
)
=
d
d
λ
(
n
ln
λ
−
λ
n
x
¯
)
=
n
λ
−
n
x
¯
{
>
0
,
0
<
λ
<
1
x
¯
,
=
0
,
λ
=
1
x
¯
,
<
0
,
λ
>
1
x
¯
.
{\displaystyle {\frac {d}{d\lambda }}\ln L(\lambda )={\frac {d}{d\lambda }}\left(n\ln \lambda -\lambda n{\overline {x}}\right)={\frac {n}{\lambda }}-n{\overline {x}}\ {\begin{cases}>0,&0<\lambda <{\frac {1}{\overline {x}}},\\[8pt]=0,&\lambda ={\frac {1}{\overline {x}}},\\[8pt]<0,&\lambda >{\frac {1}{\overline {x}}}.\end{cases}}}
λ
^
mle
=
1
x
¯
=
n
∑
i
x
i
{\displaystyle {\widehat {\lambda }}_{\text{mle}}={\frac {1}{\overline {x}}}={\frac {n}{\sum _{i}x_{i}}}}
vlerësues i paanshëm i
λ
,
{\displaystyle \lambda ,}
x
¯
{\displaystyle {\overline {x}}}
[ 3] [ 4]
1
/
λ
{\displaystyle 1/\lambda }
Zhvendosja e
λ
^
mle
{\displaystyle {\widehat {\lambda }}_{\text{mle}}}
B
≡
E
[
(
λ
^
mle
−
λ
)
]
=
λ
n
−
1
{\displaystyle B\equiv \operatorname {E} \left[\left({\widehat {\lambda }}_{\text{mle}}-\lambda \right)\right]={\frac {\lambda }{n-1}}}
λ
^
mle
∗
=
λ
^
mle
−
B
.
{\displaystyle {\widehat {\lambda }}_{\text{mle}}^{*}={\widehat {\lambda }}_{\text{mle}}-B.}
Informacioni Fisher, shënohet
I
(
λ
)
{\displaystyle {\mathcal {I}}(\lambda )}
λ
{\displaystyle \lambda }
I
(
λ
)
=
E
[
(
∂
∂
λ
log
f
(
x
;
λ
)
)
2
|
λ
]
=
∫
(
∂
∂
λ
log
f
(
x
;
λ
)
)
2
f
(
x
;
λ
)
d
x
{\displaystyle {\mathcal {I}}(\lambda )=\operatorname {E} \left[\left.\left({\frac {\partial }{\partial \lambda }}\log f(x;\lambda )\right)^{2}\right|\lambda \right]=\int \left({\frac {\partial }{\partial \lambda }}\log f(x;\lambda )\right)^{2}f(x;\lambda )\,dx}
I
(
λ
)
=
∫
0
∞
(
∂
∂
λ
log
λ
e
−
λ
x
)
2
λ
e
−
λ
x
d
x
=
∫
0
∞
(
1
λ
−
x
)
2
λ
e
−
λ
x
d
x
=
λ
−
2
.
{\displaystyle {\mathcal {I}}(\lambda )=\int _{0}^{\infty }\left({\frac {\partial }{\partial \lambda }}\log \lambda e^{-\lambda x}\right)^{2}\lambda e^{-\lambda x}\,dx=\int _{0}^{\infty }\left({\frac {1}{\lambda }}-x\right)^{2}\lambda e^{-\lambda x}\,dx=\lambda ^{-2}.}
λ
{\displaystyle \lambda }
Shpërndarja eksponenciale ndodh natyrshëm kur përshkruhen gjatësitë e kohërave ndërmjet mbërritjes në një proces homogjen Poisson .
Ndryshoret eksponenciale mund të përdoren gjithashtu për të modeluar situata ku ndodhin ngjarje të caktuara me një probabilitet konstant për njësi gjatësie, siç është largësia midis mutacioneve në një varg të ADN-së , ose midis goditjeve në rrugë në një rrugë të caktuar.
Në fizikë , nëse vëzhgoni një gaz në një temperaturë dhe shtypje fikse në një fushë gravitacionale të njëtrajtshme, lartësitë e molekulave të ndryshme ndjekin gjithashtu një shpërndarje të përafërt eksponenciale, të njohur si formula barometrike . Kjo është pasojë e vetive të entropisë të përmendura më poshtë.
^ Norton, Matthew; Khokhlov, Valentyn; Uryasev, Stan (2019). "Calculating CVaR and bPOE for common probability distributions with application to portfolio optimization and density estimation" (PDF) . Annals of Operations Research . Springer. 299 (1–2): 1281–1315. doi :10.1007/s10479-019-03373-1 . Arkivuar nga origjinali (PDF) më 31 mars 2023. Marrë më 2023-02-27 . ^ Ibe, Oliver C. (2014). Fundamentals of Applied Probability and Random Processes ISBN 9780128010358 ^ Richard Arnold Johnson; Dean W. Wichern (2007). Applied Multivariate Statistical Analysis ISBN 978-0-13-187715-3 . Marrë më 10 gusht 2012 . ^ NIST/SEMATECH e-Handbook of Statistical Methods 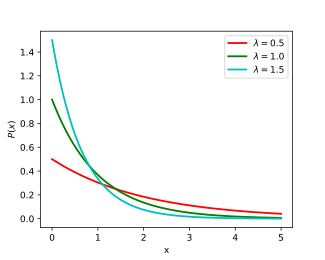

























![{\displaystyle \operatorname {E} [X]={\frac {1}{\lambda }}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9efa3ce3c964c59532609b3d6b8f01ce88f6221)
![{\displaystyle \operatorname {Var} [X]={\frac {1}{\lambda ^{2}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c450db5013b1cfdaf5ea71106c9d13834e02d61)

![{\displaystyle \operatorname {E} \left[X^{n}\right]={\frac {n!}{\lambda ^{n}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f5d3a82fbcff5a294e5360fb05b1e5f2166ec09)



![{\displaystyle \operatorname {m} [X]={\frac {\ln(2)}{\lambda }}<\operatorname {E} [X],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f19becbfbc702d8c33a9698c779384fe3f4dca1)

![{\displaystyle \left|\operatorname {E} \left[X\right]-\operatorname {m} \left[X\right]\right|={\frac {1-\ln(2)}{\lambda }}<{\frac {1}{\lambda }}=\operatorname {\sigma } [X],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e48a50d7c835e2c16f59682fe49712aa41a54d8a)


![{\displaystyle {\begin{aligned}\Pr \left(T>s+t\mid T>s\right)&={\frac {\Pr \left(T>s+t\cap T>s\right)}{\Pr \left(T>s\right)}}\\[4pt]&={\frac {\Pr \left(T>s+t\right)}{\Pr \left(T>s\right)}}\\[4pt]&={\frac {e^{-\lambda (s+t)}}{e^{-\lambda s}}}\\[4pt]&=e^{-\lambda t}\\[4pt]&=\Pr(T>t).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/126da1213459cde98ae372eae857a18183675f5a)





![{\displaystyle {\begin{aligned}{\bar {q}}_{\alpha }(X)&={\frac {1}{1-\alpha }}\int _{\alpha }^{1}q_{p}(X)dp\\&={\frac {1}{(1-\alpha )}}\int _{\alpha }^{1}{\frac {-\ln(1-p)}{\lambda }}dp\\&={\frac {-1}{\lambda (1-\alpha )}}\int _{1-\alpha }^{0}-\ln(y)dy\\&={\frac {-1}{\lambda (1-\alpha )}}\int _{0}^{1-\alpha }\ln(y)dy\\&={\frac {-1}{\lambda (1-\alpha )}}[(1-\alpha )\ln(1-\alpha )-(1-\alpha )]\\&={\frac {-\ln(1-\alpha )+1}{\lambda }}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cb6c9508565c42978ca1153dc0f6bfd0199a45c)








![{\displaystyle {\begin{aligned}f_{Z}(z)&=\int _{-\infty }^{\infty }f_{X_{1}}(x_{1})f_{X_{2}}(z-x_{1})\,dx_{1}\\&=\int _{0}^{z}\lambda _{1}e^{-\lambda _{1}x_{1}}\lambda _{2}e^{-\lambda _{2}(z-x_{1})}\,dx_{1}\\&=\lambda _{1}\lambda _{2}e^{-\lambda _{2}z}\int _{0}^{z}e^{(\lambda _{2}-\lambda _{1})x_{1}}\,dx_{1}\\&={\begin{cases}{\dfrac {\lambda _{1}\lambda _{2}}{\lambda _{2}-\lambda _{1}}}\left(e^{-\lambda _{1}z}-e^{-\lambda _{2}z}\right)&{\text{ if }}\lambda _{1}\neq \lambda _{2}\\[4pt]\lambda ^{2}ze^{-\lambda z}&{\text{ if }}\lambda _{1}=\lambda _{2}=\lambda .\end{cases}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2db15dda49fe8482485a68c9d7c9b1c1d46ee95)





















































![{\displaystyle {\frac {d}{d\lambda }}\ln L(\lambda )={\frac {d}{d\lambda }}\left(n\ln \lambda -\lambda n{\overline {x}}\right)={\frac {n}{\lambda }}-n{\overline {x}}\ {\begin{cases}>0,&0<\lambda <{\frac {1}{\overline {x}}},\\[8pt]=0,&\lambda ={\frac {1}{\overline {x}}},\\[8pt]<0,&\lambda >{\frac {1}{\overline {x}}}.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65ec59bc9ccff1952291621e3eccc741ee1341a2)





![{\displaystyle B\equiv \operatorname {E} \left[\left({\widehat {\lambda }}_{\text{mle}}-\lambda \right)\right]={\frac {\lambda }{n-1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6df9c9d7b6d1a8ffc31748e7cdf0cc750b442e4)


![{\displaystyle {\mathcal {I}}(\lambda )=\operatorname {E} \left[\left.\left({\frac {\partial }{\partial \lambda }}\log f(x;\lambda )\right)^{2}\right|\lambda \right]=\int \left({\frac {\partial }{\partial \lambda }}\log f(x;\lambda )\right)^{2}f(x;\lambda )\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c70bd835b54bb1b7f344dbf1f04d170bd1d4852)
