Teorema e 4 ngjyrave

Example of a four-colored map

Në matematikë, teorema me katër ngjyra, ose teorema e hartës me katër ngjyra, thotë se jo më shumë se katër ngjyra janë të nevojshme për të ngjyrosur rajonet e çdo harte në mënyrë që asnjë rajon fqinj të mos ketë të njëjtën ngjyrë. Ngjitur do të thotë që dy rajone ndajnë një segment të përbashkët të kurbës kufitare, jo thjesht një cep ku takohen tre ose më shumë rajone. Ishte teorema e parë kryesore që u vërtetua duke përdorur një kompjuter. Fillimisht, kjo provë nuk u pranua nga të gjithë matematikanët, sepse prova e asistuar nga kompjuteri ishte e pamundur që njeriu të kontrollonte me dorë. Që atëherë prova ka fituar pranim të gjerë, edhe pse disa dyshues mbeten.

Teorema e katër ngjyrave u vërtetua në 1976 nga Kenneth Appel dhe Wolfgang Haken pas shumë provave dhe kundërshembujve të rremë (ndryshe nga teorema e pesë ngjyrave, e provuar në vitet 1800, e cila thotë se pesë ngjyra janë të mjaftueshme për të ngjyrosur një hartë). Për të larguar çdo dyshim të mbetur në lidhje me provën e Appel-Haken, një provë më e thjeshtë duke përdorur të njëjtat ide dhe ende duke u mbështetur në kompjuterë u botua në 1997 nga Robertson, Sanders, Seymour dhe Thomas. Në vitin 2005, teorema u vërtetua gjithashtu nga Georges Gonthier me softuer të përgjithshëm për të vërtetuar teorema.

Formulimi i saktë i teoremës

Në terma grafik-teorik, teorema thotë se për grafikun planar pa qark $G$, numri i tij kromatik është $\chi (G)\leq 4$.

Deklarata intuitive e teoremës së katër ngjyrave - "duke pasur parasysh çdo ndarje të një plani në rajone të afërta, rajonet mund të ngjyrosen duke përdorur më së shumti katër ngjyra në mënyrë që asnjë rajon fqinj të mos ketë të njëjtën ngjyrë" - duhet të interpretohet në mënyrë të përshtatshme për të qenë e saktë.

A four-coloring of a map of the states of the United States (ignoring lakes and oceans).

Së pari, rajonet janë ngjitur nëse ndajnë një segment kufitar; dy rajone që ndajnë vetëm pika kufitare të izoluara nuk konsiderohen fqinjë. Së dyti, rajonet e çuditshme, si ato me sipërfaqe të kufizuar, por me perimetër pafundësisht të gjatë, nuk lejohen; hartat me rajone të tilla mund të kërkojnë më shumë se katër ngjyra. (Për të qenë të sigurt, ne mund të kufizojmë në rajonet, kufijtë e të cilëve përbëhen nga shumë segmente të vijës së drejtë. Lejohet që një rajon të rrethojë tërësisht një ose më shumë rajone të tjera.) Vini re se nocioni i "rajonit të afërt" (teknikisht: nëngrup i hapur i lidhur i aeroplanit) nuk është i njëjtë me atë të një "vendi" në hartat e rregullta, pasi vendet nuk duhet të jenë të afërta (p.sh., Provinca Cabinda si pjesë e Angolës, Nakhchivan si pjesë e Azerbajxhanit, Kaliningrad si pjesë e Rusisë dhe Alaska. si pjesë e Shteteve të Bashkuara nuk janë të ngjitura). Nëse kërkojmë që i gjithë territori i një vendi të marrë të njëjtën ngjyrë, atëherë katër ngjyra nuk janë gjithmonë të mjaftueshme. Për shembull, merrni parasysh një hartë të thjeshtuar:

Në këtë hartë, dy rajonet e emërtuara A i përkasin të njëjtit shtet. Nëse do të donim që ato rajone të merrnin të njëjtën ngjyrë, atëherë do të kërkoheshin pesë ngjyra, pasi të dy rajonet A së bashku janë ngjitur me katër rajone të tjera, secila prej të cilave është ngjitur me të gjitha të tjerat. Detyrimi i dy zonave të veçanta që të kenë të njëjtën ngjyrë mund të modelohet duke shtuar një 'dorezë' që i bashkon ato jashtë planit.

Një ndërtim i tillë e bën problemin të barabartë me ngjyrosjen e një harte në një torus (një sipërfaqe e gjinisë 1), e cila kërkon deri në 7 ngjyra për një hartë arbitrare. Një ndërtim i ngjashëm zbatohet gjithashtu nëse një ngjyrë e vetme përdoret për zona të shumta të shkëputura, si për trupat ujorë në hartat reale, ose ka më shumë vende me territore të shkëputura. Në raste të tilla mund të kërkohen më shumë ngjyra me një gjini në rritje të një sipërfaqeje që rezulton. (Shih seksionin Përgjithësimet më poshtë.)

A map with four regions, and the corresponding planar graph with four vertices.

Një deklaratë më e thjeshtë e teoremës përdor teorinë e grafit. Grupi i rajoneve të një harte mund të përfaqësohet në mënyrë më abstrakte si një graf i padrejtuar që ka një kulm për çdo rajon dhe një skaj për çdo çift rajonesh që ndajnë një segment kufitar. Ky grafik është planar: ai mund të vizatohet në rrafsh pa kryqëzime duke vendosur çdo kulm në një vend të zgjedhur arbitrarisht brenda rajonit të cilit i përgjigjet, dhe duke vizatuar skajet si kthesa pa kryqëzime që çojnë nga kulmi i një rajoni, përgjatë një kulmi të përbashkët. segmenti kufitar, në kulmin e një rajoni ngjitur. Në të kundërt çdo grafik planar mund të formohet nga një hartë në këtë mënyrë. Në terminologjinë e teorisë së grafit, teorema me katër ngjyra thotë se kulmet e çdo grafi planar mund të ngjyrosen me maksimum katër ngjyra, në mënyrë që asnjë kulm fqinj të mos marrë të njëjtën ngjyrë, ose shkurt:

Çdo grafik planar është me katër ngjyra.

Historia

Përpjekjet e hershme të provës

Letter of De Morgan to Hamilton, 23 Oct. 1852

Me sa dihet, hamendësimi u propozua për herë të parë më 23 tetor 1852, kur Francis Guthrie, duke u përpjekur të ngjyroste hartën e qarqeve të Anglisë, vuri re se duheshin vetëm katër ngjyra të ndryshme. Në atë kohë, vëllai i Guthrie, Frederick, ishte student i Augustus De Morgan (ish-këshilltari i Francis) në University College London. Françesku pyeti Frederikun në lidhje me të, i cili më pas e çoi në De Morgan (Francis Guthrie u diplomua më vonë në 1852 dhe më vonë u bë profesor i matematikës në Afrikën e Jugut). Sipas De Morgan:

"Një student i imi [Guthrie] më kërkoi sot t'i jepja një arsye për një fakt që nuk e dija se ishte fakt—dhe nuk e di ende. Ai thotë se nëse një figurë është e tillë, sa të ndarë dhe ndarjet me ngjyra të ndryshme kështu se figurat me çdo pjesë të vijës së përbashkët kufitare janë me ngjyra të ndryshme - mund të kërkohen katër ngjyra, por jo më shumë - në vijim është rasti i tij në të cilin kërkohen katër ngjyra. Pyetja nuk mund të shpiket një domosdoshmëri për pesë ose më shumë…" (Wilson 2014, f. 18)

"FG", ndoshta një nga dy Guthries, e botoi pyetjen në The Athenaeum në 1854, dhe De Morgan e shtroi përsëri pyetjen në të njëjtën revistë në 1860. Një tjetër referencë e hershme e botuar nga Arthur Cayley (1879) nga ana e saj i jep hamendjes De Morgan. Pati disa përpjekje të hershme të dështuara për të vërtetuar teoremën. De Morgan besonte se kjo rrjedh nga një fakt i thjeshtë për katër rajone, megjithëse ai nuk besonte se ai fakt mund të nxirrej nga fakte më elementare.

Kjo lind në mënyrën e mëposhtme. Ne kurrë nuk kemi nevojë për katër ngjyra në një lagje, përveç nëse ka katër qarqe, secila prej të cilave ka vija kufitare të përbashkëta me secilën nga tre të tjerat. Një gjë e tillë nuk mund të ndodhë me katër zona nëse një ose më shumë prej tyre nuk përfshihen nga pjesa tjetër; dhe ngjyra e përdorur për qarkun e mbyllur është kështu e lirë për të vazhduar me të. Tani ky parim, që katër zona nuk mund të kenë secila kufi të përbashkët me të tre të tjerat pa i mbyllur, ne besojmë plotësisht, nuk është i aftë të demonstrojë diçka më të dukshme dhe më elementare; duhet të qëndrojë si postulat.

Një provë e propozuar u dha nga Alfred Kempe në 1879, e cila u vlerësua gjerësisht; një tjetër u dha nga Peter Guthrie Tait në 1880. Vetëm në vitin 1890 prova e Kempe u tregua e pasaktë nga Percy Heawood, dhe në 1891, prova e Tait u tregua e pasaktë nga Julius Petersen - secila provë e rreme qëndroi e pakundërshtueshme për 11 vjet.

Në 1890, përveç ekspozimit të të metave në provën e Kempe, Heawood vërtetoi teoremën e pesë ngjyrave dhe përgjithësoi hamendjen e katër ngjyrave në sipërfaqet e gjinisë arbitrare.

Tait, në 1880, tregoi se teorema e katër ngjyrave është ekuivalente me pohimin se një lloj i caktuar grafiku (i quajtur snark në terminologjinë moderne) duhet të jetë jo planar.

Në vitin 1943, Hugo Hadwiger formuloi hamendësimin Hadwiger, një përgjithësim i gjerë i problemit me katër ngjyra që mbetet ende i pazgjidhur.

Prova me kompjuter

Gjatë viteve 1960 dhe 1970, matematikani gjerman Heinrich Heesch zhvilloi metoda të përdorimit të kompjuterëve për të kërkuar një provë. Veçanërisht ai ishte i pari që përdori shkarkimin për të vërtetuar teoremën, e cila doli të ishte e rëndësishme në pjesën e pashmangshmërisë së provës së mëvonshme Appel-Haken. Ai gjithashtu zgjeroi konceptin e reduktueshmërisë dhe, së bashku me Ken Durre, zhvilloi një test kompjuterik për të. Fatkeqësisht, në këtë moment kritik, ai nuk ishte në gjendje të siguronte kohën e nevojshme të superkompjuterit për të vazhduar punën e tij.

Të tjerë morën metodat e tij, duke përfshirë qasjen e tij me kompjuter. Ndërsa ekipet e tjera të matematikanëve po garonin për të plotësuar provat, Kenneth Appel dhe Wolfgang Haken në Universitetin e Illinois njoftuan, më 21 qershor 1976, se kishin vërtetuar teoremën. Ata u ndihmuan në disa punë algoritmike nga John A. Koch.

Nëse hamendësimi me katër ngjyra do të ishte i rremë, do të kishte të paktën një hartë me numrin më të vogël të mundshëm të rajoneve që kërkon pesë ngjyra. Prova tregoi se një kundërshembull i tillë minimal nuk mund të ekzistojë, nëpërmjet përdorimit të dy koncepteve teknike:

1. Një grup i pashmangshëm është një grup konfigurimesh të tilla që çdo hartë që plotëson disa kushte të nevojshme për të qenë një trekëndëshim minimal jo me 4 ngjyra (si p.sh. të kesh shkallë minimale 5) duhet të ketë të paktën një konfigurim nga ky grup.
2. Një konfigurim i reduktueshëm është një rregullim i vendeve që nuk mund të ndodhin në një kundërshembull minimal. Nëse një hartë përmban një konfigurim të reduktueshëm, harta mund të reduktohet në një hartë më të vogël. Kjo hartë më e vogël ka kushtin që nëse mund të ngjyroset me katër ngjyra, kjo vlen edhe për hartën origjinale. Kjo nënkupton që nëse harta origjinale nuk mund të ngjyroset me katër ngjyra, atëherë harta më e vogël nuk mundet dhe kështu harta origjinale nuk është minimale.

Duke përdorur rregullat dhe procedurat matematikore të bazuara në vetitë e konfigurimeve të reduktueshme, Appel dhe Haken gjetën një grup të pashmangshëm konfigurimesh të reduktueshme, duke vërtetuar kështu se një kundërshembull minimal ndaj hamendjes me katër ngjyra nuk mund të ekzistonte. Prova e tyre reduktoi pafundësinë e hartave të mundshme në 1,834 konfigurime të reduktueshme (më vonë u reduktuan në 1,482) të cilat duhej të kontrolloheshin një nga një nga kompjuteri dhe zgjatën mbi një mijë orë. Kjo pjesë e reduktueshmërisë së punës u kontrollua në mënyrë të pavarur me programe dhe kompjuterë të ndryshëm. Megjithatë, pjesa e pashmangshme e provës u verifikua në mbi 400 faqe mikrofishe, të cilat duhej të kontrolloheshin me dorë me ndihmën e vajzës së Haken, Dorothea Blostein (Appel & Haken 1989).

Njoftimi i Appel dhe Haken u raportua gjerësisht nga mediat e lajmeve në mbarë botën, dhe departamenti i matematikës në Universitetin e Illinois përdori një vulë postare ku thuhej "Katër ngjyrat mjaftojnë". Në të njëjtën kohë, natyra e pazakontë e provës - ishte teorema e parë kryesore që u vërtetua me ndihmë të gjerë kompjuterike - dhe kompleksiteti i pjesës së verifikueshme nga njeriu ngjalli polemika të konsiderueshme (Wilson 2014).

Në fillim të viteve 1980, u përhapën thashethemet për një të metë në provat e Appel-Haken. Ulrich Schmidt në RWTH Aachen kishte ekzaminuar provat e Appel dhe Haken për tezën e tij të masterit që u botua në 1981 (Wilson 2014, 225). Ai kishte kontrolluar rreth 40% të pjesës së pashmangshmërisë dhe gjeti një gabim të rëndësishëm në procedurën e shkarkimit (Appel & Haken 1989). Në vitin 1986, Appel dhe Haken iu kërkua nga redaktori i Mathematical Intelligencer të shkruanin një artikull duke adresuar thashethemet për të metat në provat e tyre. Ata u përgjigjën se thashethemet ishin për shkak të një "interpretimi të gabuar të rezultateve të [Schmidt]" dhe të detyruar me një artikull të detajuar (Wilson 2014, 225–226). Opusi i tyre i madh, Çdo Hartë Planare është me Katër ngjyra, një libër që pretendon një provë të plotë dhe të detajuar (me një shtesë mikrofishe prej mbi 400 faqesh), u shfaq në 1989; ai shpjegoi dhe korrigjoi gabimin e zbuluar nga Schmidt si dhe disa gabime të tjera të gjetura nga të tjerët (Appel & Haken 1989).

Thjeshtimi dhe verifikimi

Që nga vërtetimi i teoremës, janë gjetur algoritme efikase për hartat me 4 ngjyra që kërkojnë vetëm kohë O(n²), ku n është numri i kulmeve. Në vitin 1996, Neil Robertson, Daniel P. Sanders, Paul Seymour dhe Robin Thomas krijuan një algoritëm të kohës kuadratike, duke u përmirësuar në një algoritëm të kohës kuartike bazuar në provën e Appel dhe Haken. Kjo provë e re është e ngjashme me atë të Appel dhe Haken, por më efikase sepse zvogëlon kompleksitetin e problemit dhe kërkon kontrollimin e vetëm 633 konfigurimeve të reduktueshme. Të dyja pjesët e pashmangshmërisë dhe reduktueshmërisë së kësaj prove të re duhet të ekzekutohen me kompjuter dhe janë jopraktike për t'u kontrolluar me dorë. Në vitin 2001, të njëjtët autorë shpallën një provë alternative, duke vërtetuar hamendësimin snark. Megjithatë, kjo provë mbetet e pabotuar.

Në vitin 2005, Benjamin Werner dhe Georges Gonthier zyrtarizuan një provë të teoremës brenda asistentit të provës Coq. Kjo hoqi nevojën për t'u besuar programeve të ndryshme kompjuterike të përdorura për të verifikuar raste të veçanta; është e nevojshme vetëm t'i besoni kernelit Coq.

Përmbledhje e ideve provuese

Diskutimi i mëposhtëm është një përmbledhje e bazuar në hyrjen e Every Planar Map is Four Colorable (Appel & Haken 1989). Edhe pse me të meta, prova origjinale e supozuar e Kempe për teoremën e katër ngjyrave siguroi disa nga mjetet bazë të përdorura më vonë për ta vërtetuar atë. Shpjegimi këtu është riformuluar në termat e formulimit të teorisë moderne të grafikut më sipër.

Argumenti i Kempes shkon si më poshtë. Së pari, nëse rajonet planare të ndara nga grafiku nuk janë trekëndore, d.m.th. nuk kanë saktësisht tre skaje në kufijtë e tyre, ne mund të shtojmë skaje pa futur kulme të reja në mënyrë që të bëjmë çdo rajon trekëndor, duke përfshirë rajonin e jashtëm të pakufishëm. Nëse ky grafik trekëndësh është i ngjyrueshëm duke përdorur katër ngjyra ose më pak, i tillë është edhe grafiku origjinal pasi i njëjti ngjyrosje është i vlefshëm nëse skajet hiqen. Pra, mjafton të vërtetohet teorema e katër ngjyrave për grafët trekëndësh për ta vërtetuar atë për të gjithë grafët planarë, dhe pa humbur përgjithësinë supozojmë se grafiku është trekëndor.

Supozoni se v, e dhe f janë numri i kulmeve, skajeve dhe rajoneve (fytyrave). Meqenëse çdo rajon është trekëndor dhe secila skaj ndahet nga dy rajone, kemi atë 2e = 3f. Kjo së bashku me formulën e Euler-it, v − e + f = 2, mund të përdoret për të treguar se 6v − 2e = 12. Tani, shkalla e një kulmi është numri i skajeve që i afrohen. Nëse vn është numri i kulmeve të shkallës n dhe D është shkalla maksimale e çdo kulmi,

$6v-2e=6\sum _{i=1}^{D}v_{i}-\sum _{i=1}^{D}iv_{i}=\sum _{i=1}^{D}(6-i)v_{i}=12.$

Por meqenëse 12 > 0 dhe 6 − i ≤ 0 për të gjithë i ≥ 6, kjo tregon se ka të paktën një kulm të shkallës 5 ose më pak.

Nëse ekziston një grafik që kërkon 5 ngjyra, atëherë ekziston një grafik i tillë minimal, ku heqja e çdo kulmi e bën atë të katërngjyrshëm. Quajeni këtë grafik G. Atëherë G nuk mund të ketë një kulm të shkallës 3 ose më pak, sepse nëse d(v) ≤ 3, ne mund të heqim v nga G, të ngjyrosim grafikun më të vogël, pastaj të shtojmë mbrapa v dhe të zgjerojmë katërngjyrosjen. ndaj tij duke zgjedhur një ngjyrë të ndryshme nga fqinjët e saj.

A graph containing a Kempe chain consisting of alternating blue and red vertices

Kempe gjithashtu tregoi saktë se G nuk mund të ketë kulm të shkallës 4. Si më parë heqim kulmin v dhe ngjyrosim kulmet e mbetura. Nëse të katër fqinjët e v janë me ngjyra të ndryshme, le të themi e kuqe, jeshile, blu dhe e verdhë në rendin e akrepave të orës, ne kërkojmë një rrugë alternative të kulmeve me ngjyrë të kuqe dhe blu që bashkojnë fqinjët e kuq dhe blu. Një rrugë e tillë quhet zinxhir Kempe. Mund të ketë një zinxhir Kempe që bashkon fqinjët e kuq dhe blu dhe mund të ketë një zinxhir Kempe që bashkon fqinjët e gjelbër dhe të verdhë, por jo të dyja, pasi këto dy shtigje domosdoshmërisht do të kryqëzoheshin dhe kulmi ku kryqëzohen nuk mund të ngjyroset. Supozoni se janë fqinjët e kuq dhe blu që nuk janë të lidhur me zinxhirë së bashku. Eksploroni të gjitha kulmet e bashkangjitura me fqinjin e kuq nga shtigjet e alternuara të kuqe-blu dhe më pas ndryshoni ngjyrat e kuqe dhe blu në të gjitha këto kulme. Rezultati është ende një ngjyrosje e vlefshme me katër ngjyra, dhe v tani mund të shtohet përsëri dhe të ngjyroset e kuqe.

Kjo lë vetëm rastin kur G ka një kulm të shkallës 5; por argumenti i Kempes ishte me të meta për këtë rast. Heawood vuri re gabimin e Kempe dhe gjithashtu vuri re se nëse dikush do të ishte i kënaqur me vërtetimin se nevojiten vetëm pesë ngjyra, mund të kalonte në argumentin e mësipërm (duke ndryshuar vetëm se kundërshembulli minimal kërkon 6 ngjyra) dhe të përdorte zinxhirët Kempe në situatën e shkallës 5 për të vërtetuar teorema me pesë ngjyra.

Në çdo rast, për t'u marrë me këtë rast të kulmit të shkallës 5 kërkon një nocion më të ndërlikuar sesa heqja e një kulmi. Përkundrazi, forma e argumentit përgjithësohet për të marrë në konsideratë konfigurimet, të cilat janë nëngrafë të lidhur të G me shkallën e çdo kulmi (në G) të specifikuar. Për shembull, rasti i përshkruar në situatën e kulmit të shkallës 4 është konfigurimi që përbëhet nga një kulm i vetëm i etiketuar se ka shkallën 4 në G. Si më sipër, mjafton të tregohet se nëse konfigurimi hiqet dhe grafiku i mbetur ka katër ngjyra, atëherë ngjyrosja mund të modifikohet në atë mënyrë që kur konfigurimi të rishitet, katërngjyrosja mund të zgjerohet edhe në të. Një konfigurim për të cilin kjo është e mundur quhet konfigurim i reduktueshëm. Nëse të paktën një nga një grup konfigurimesh duhet të ndodhë diku në G, ai grup quhet i pashmangshëm. Argumenti i mësipërm filloi duke dhënë një grup të pashmangshëm prej pesë konfigurimesh (një kulm i vetëm me shkallën 1, një kulm i vetëm me shkallën 2, ..., një kulm i vetëm me shkallën 5) dhe më pas vazhdoi të tregojë se 4 të parat janë të reduktueshme; për të shfaqur një grup të pashmangshëm konfigurimesh ku çdo konfigurim në grup është i reduktueshëm do të vërtetonte teoremën.

Për shkak se G është trekëndësh, shkalla e secilës kulm në një konfigurim është e njohur dhe të gjitha skajet e brendshme të konfigurimit janë të njohura, numri i kulmeve në G ngjitur me një konfigurim të caktuar është i fiksuar dhe ato bashkohen në një cikël. Këto kulme formojnë unazën e konfigurimit; një konfigurim me k kulme në unazën e tij është një konfigurim me unazë k, dhe konfigurimi së bashku me unazën e tij quhet konfigurim i rrethuar. Si në rastet e thjeshta të mësipërme, mund të numërohen të gjitha katër ngjyrat e dallueshme të unazës; çdo ngjyrosje që mund të zgjerohet pa modifikuar në një ngjyrosje të konfigurimit quhet fillimisht i mirë. Për shembull, konfigurimi me një kulm të mësipërm me 3 ose më pak fqinjë ishte fillimisht i mirë. Në përgjithësi, grafiku rrethues duhet të ringjyrohet sistematikisht për ta kthyer ngjyrosjen e unazës në një ngjyrë të mirë, siç u veprua në rastin më sipër ku kishte 4 fqinjë; për një konfigurim të përgjithshëm me një unazë më të madhe, kjo kërkon teknika më komplekse. Për shkak të numrit të madh të katër ngjyrave të dallueshme të unazës, ky është hapi kryesor që kërkon ndihmë kompjuterike.

Së fundi, mbetet për të identifikuar një grup të pashmangshëm konfigurimesh që mund të reduktohen nga kjo procedurë. Metoda kryesore e përdorur për të zbuluar një grup të tillë është metoda e shkarkimit. Ideja intuitive e shkarkimit është të konsiderohet grafiku planar si një rrjet elektrik. Fillimisht "ngarkesa elektrike" pozitive dhe negative shpërndahet midis kulmeve në mënyrë që totali të jetë pozitiv.

Kujtoni formulën e mësipërme:

$\sum _{i=1}^{D}(6-i)v_{i}=12.$

Çdo kulm i caktohet një ngarkesë fillestare prej 6-deg(v). Më pas njeriu "rrjedh" ngarkesën duke rishpërndarë sistematikisht ngarkesën nga një kulm në kulmet fqinje sipas një sërë rregullash, procedurën e shkarkimit. Meqenëse ngarkesa ruhet, disa kulme ende kanë ngarkesë pozitive. Rregullat kufizojnë mundësitë për konfigurimin e kulmeve të ngarkuara pozitivisht, kështu që numërimi i të gjitha konfigurimeve të tilla të mundshme jep një grup të pashmangshëm.

Për sa kohë që një pjesë e grupit të pashmangshëm nuk është i reduktueshëm, procedura e shkarkimit modifikohet për ta eliminuar atë (duke futur konfigurime të tjera). Procedura përfundimtare e shkarkimit të Appel dhe Haken ishte jashtëzakonisht komplekse dhe, së bashku me një përshkrim të grupit të konfigurimit të pashmangshëm që rezultoi, mbushi një vëllim prej 400 faqesh, por konfigurimet që gjeneronte mund të kontrolloheshin mekanikisht për të qenë të reduktueshme. Verifikimi i vëllimit që përshkruan vetë grupin e konfigurimit të pashmangshëm është bërë nga rishikimi i kolegëve gjatë një periudhe disavjeçare.

Një detaj teknik që nuk diskutohet këtu, por që kërkohet për të përfunduar provën është reduktueshmëria e zhytjes.

Mospranimet e rreme

Teorema e katër ngjyrave ka qenë e njohur për tërheqjen e një numri të madh provash dhe mohimesh të rreme në historinë e saj të gjatë. Në fillim, The New York Times refuzoi si çështje politike të raportonte mbi provën e Appel-Haken, nga frika se provat do të tregoheshin të rreme si ato para saj (Wilson 2014). Disa prova të supozuara, si ato të Kempe dhe Tait të përmendura më lart, qëndruan nën shqyrtimin publik për më shumë se një dekadë përpara se të hidheshin poshtë. Por shumë të tjera, me autorë amatorë, nuk u botuan kurrë fare.

The map (left) has been colored with five colors, but for example four of the ten regions can be changed to obtain a coloring with only four colors (right).

Në përgjithësi, kundërshembullët më të thjeshtë, megjithëse të pavlefshëm, përpiqen të krijojnë një rajon që prek të gjitha rajonet e tjera. Kjo detyron zonat e mbetura të ngjyrosen vetëm me tre ngjyra. Për shkak se teorema e katër ngjyrave është e vërtetë, kjo është gjithmonë e mundur; megjithatë, për shkak se personi që vizaton hartën është i fokusuar në një rajon të madh, ata nuk arrijnë të vërejnë se rajonet e mbetura në fakt mund të ngjyrosen me tre ngjyra.

Ky truk mund të përgjithësohet: ka shumë harta ku nëse zgjidhen ngjyrat e disa rajoneve paraprakisht, bëhet e pamundur të ngjyrosësh rajonet e mbetura pa i kaluar katër ngjyra. Një verifikues i rastësishëm i kundërshembullit mund të mos mendojë të ndryshojë ngjyrat e këtyre rajoneve, në mënyrë që kundërshembulli të duket sikur është i vlefshëm.

Ndoshta një efekt që qëndron në themel të këtij keqkuptimi të zakonshëm është fakti se kufizimi i ngjyrave nuk është kalimtar: një rajon duhet vetëm të ngjyroset ndryshe nga rajonet që prek drejtpërdrejt, jo rajonet që prekin rajonet që ai prek. Nëse ky do të ishte kufizimi, grafikët planar do të kërkonin një numër të madh ngjyrash në mënyrë arbitrare.

Mohimet e tjera të rreme shkelin supozimet e teoremës, si p.sh. përdorimi i një rajoni që përbëhet nga pjesë të shumta të shkëputura ose moslejimi i prekjes së rajoneve të së njëjtës ngjyrë në një pikë.

Me tre ngjyra

Proof without words that a map of US states needs at least four colors, even ignoring the quadripoint

Ndërsa çdo hartë planare mund të ngjyroset me katër ngjyra, është kompleksiteti NP-komplet për të vendosur nëse një hartë planare arbitrare mund të ngjyroset vetëm me tre ngjyra.

Një hartë kubike mund të ngjyroset vetëm me tre ngjyra nëse dhe vetëm nëse çdo rajon i brendshëm ka një numër çift rajonesh fqinje. Në shembullin e hartës së shteteve të SHBA, Misuri (MO) pa dalje në det ka tetë fqinjë (një numër çift): duhet të jetë me ngjyra të ndryshme nga të gjithë, por fqinjët mund të alternojnë ngjyrat, kështu që kjo pjesë e hartës ka nevojë vetëm për tre ngjyra. Sidoqoftë, Nevada (NV) pa dalje në det ka pesë fqinjë (një numër tek): njëri nga fqinjët duhet të jetë me ngjyrë të ndryshme nga ai dhe të gjithë të tjerët, kështu që këtu nevojiten katër ngjyra.

Përgjithësimet

Grafikët e pafund

By joining the single arrows together and the double arrows together, one obtains a torus with seven mutually touching regions; therefore seven colors are necessary

Teorema e katër ngjyrave zbatohet jo vetëm për grafikët planarë të fundëm, por edhe për grafët e pafundëm që mund të vizatohen pa kryqëzime në rrafsh, dhe akoma më në përgjithësi për grafët e pafundëm (mundësisht me një numër të panumërueshëm kulmesh) për të cilët çdo nëngraf i fundëm është planare. Për të vërtetuar këtë, mund të kombinohet një vërtetim i teoremës për grafët planarë të fundëm me teoremën e De Bruijn–Erdős duke thënë se, nëse çdo nëngraf i fundëm i një grafi të pafundëm është k-ngjyrueshëm, atëherë i gjithë grafi është gjithashtu k-ngjyrshëm Nash- Williams (1967). Kjo mund të shihet gjithashtu si një pasojë e menjëhershme e teoremës së kompaktësisë së Kurt Gödel për logjikën e rendit të parë, thjesht duke shprehur ngjyrueshmërinë e një grafi të pafund me një grup formulash logjike.

Sipërfaqet më të larta

Mund të merret në konsideratë edhe problemi i ngjyrosjes në sipërfaqe të ndryshme nga rrafshi. Problemi në sferë ose cilindër është i barabartë me atë në aeroplan. Për sipërfaqet e mbyllura (të orientueshme ose jo të orientueshme) me gjini pozitive, numri maksimal p i ngjyrave të nevojshme varet nga karakteristika Euler χ e sipërfaqes sipas formulës

$p=\left\lfloor {\frac {7+{\sqrt {49-24\chi }}}{2}}\right\rfloor ,$

ku kllapat më të jashtme tregojnë funksionin e dyshemesë. Përndryshe, për një sipërfaqe të orientueshme formula mund të jepet për sa i përket gjinisë së një sipërfaqeje, g:

$p=\left\lfloor {\frac {7+{\sqrt {1+48g}}}{2}}\right\rfloor .$

Kjo formulë, hamendja e Heawood-it, u propozua nga PJ Heawood në 1890 dhe, pas kontributeve të disa njerëzve, u vërtetua nga Gerhard Ringel dhe JWT Youngs në 1968. Përjashtimi i vetëm nga formula është shishja Klein, e cila ka karakteristikën Euler 0 (prandaj formula jep p = 7) por kërkon vetëm 6 ngjyra, siç tregohet nga Philip Franklin në 1934.

Për shembull, torus ka karakteristikën e Euler-it χ = 0 (dhe gjininë g = 1) dhe kështu p = 7, kështu që jo më shumë se 7 ngjyra nevojiten për të ngjyrosur çdo hartë në një torus. Ky kufi i sipërm prej 7 është i mprehtë: disa poliedra toroidalë si poliedri Szilassi kërkojnë shtatë ngjyra.

Një shirit Möbius kërkon gjashtë ngjyra (Tietze 1910) si dhe grafikët 1-planar (grafikë të vizatuar më së shumti me një kryqëzim të thjeshtë për buzë) (Borodin 1984). Nëse të dyja kulmet dhe faqet e një grafiku planar janë të ngjyrosura, në mënyrë të tillë që asnjë dy kulme, fytyra ose çift kulme-fytyrë ngjitur të mos kenë të njëjtën ngjyrë, atëherë përsëri nevojiten maksimumi gjashtë ngjyra (Borodin 1984).

• 
  A radially symmetric 7-colored torus – regions of the same colour wrap around along dotted lines
• 
  An 8-coloured double torus (genus-two surface) – bubbles denotes unique combination of two regions
• 
  A 6-colored Klein bottle
• 
  Tietze's subdivision of a Möbius strip into six mutually adjacent regions, requiring six colors. The vertices and edges of the subdivision form an embedding of Tietze's graph onto the strip.
• 
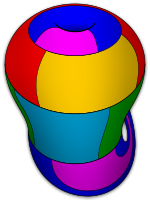
  Interactive Szilassi polyhedron model with each of 7 faces adjacent to every other – in the SVG image, move the mouse to rotate it
• 
  Proof without words that the number of colours needed is unbounded in three or more dimensions

Rajone të ngurta

Nuk ka një shtrirje të dukshme të rezultatit të ngjyrosjes në rajone të ngurta tre-dimensionale. Duke përdorur një grup prej n shufrash fleksibël, mund të organizohet që çdo shufër të prekë çdo shufër tjetër. Më pas grupi do të kërkonte n ngjyra, ose n+1 duke përfshirë hapësirën boshe që prek gjithashtu çdo shufër. Numri n mund të merret si çdo numër i plotë, aq i madh sa të dëshirohet. Shembuj të tillë ishin të njohur për Fredrick Guthrie në 1880 (Wilson 2014). Edhe për kuboidët paralelë me boshtin (që konsiderohen të afërt kur dy kuboide ndajnë një zonë kufitare dy-dimensionale) mund të jetë i nevojshëm një numër i pakufishëm ngjyrash (Reed & Allwright 2008; Magnant & Martin (2011)).

Lidhja me fushat e tjera të matematikës

Dror Bar-Natan dha një deklaratë në lidhje me algjebrat e Gënjeshtrës dhe invariantet e Vassiliev, e cila është ekuivalente me teoremën e katër ngjyrave.

Përdorimi jashtë matematikës

Pavarësisht motivimit nga ngjyrosja e hartave politike të vendeve, teorema nuk është me interes të veçantë për hartografët. Sipas një artikulli të historianit të matematikës Kenneth May, "Hartat që përdorin vetëm katër ngjyra janë të rralla dhe ato që përdorin zakonisht vetëm tre. Librat mbi hartografinë dhe historinë e hartimit të hartave nuk përmendin vetinë e katër ngjyrave" (Wilson 2014, 2). Teorema gjithashtu nuk garanton kërkesën e zakonshme hartografike që rajonet jo të afërta të të njëjtit vend (siç është enklava e Alaskës dhe pjesa tjetër e Shteteve të Bashkuara) të jenë të ngjyrosura në mënyrë identike.

Shiko gjithashtu

• Rrjeti Apollonian
• Teorema me pesë ngjyra
• Ngjyrosja e grafikut
• Teorema e Grötzsch-it: grafikët planarë pa trekëndësh janë me 3 ngjyra.
• Problemi Hadwiger–Nelson: sa ngjyra nevojiten për të ngjyrosur rrafshin në mënyrë që asnjë pikë në distancë njësi të mos ketë të njëjtën ngjyrë?

Referencat

==

• Allaire, Frank (1978), "Another proof of the four colour theorem. I.", përmbledhur nga D. McCarthy; H. C. Williams (red.), Proceedings, 7th Manitoba Conference on Numerical Mathematics and Computing, Congr. Numer., vëll. 20, Winnipeg, Man.: Utilitas Mathematica Publishing, Inc., fq. 3–72, ISBN 0-919628-20-6, MR 0535003 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Appel, Kenneth; Haken, Wolfgang (1977), "Every Planar Map is Four Colorable. I. Discharging", Illinois Journal of Mathematics, 21 (3): 429–490, doi:10.1215/ijm/1256049011, MR 0543792 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Appel, Kenneth; Haken, Wolfgang; Koch, John (1977), "Every Planar Map is Four Colorable. II. Reducibility", Illinois Journal of Mathematics, 21 (3): 491–567, doi:10.1215/ijm/1256049012, MR 0543793 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Appel, Kenneth; Haken, Wolfgang (tetor 1977), "Solution of the Four Color Map Problem", Scientific American, vëll. 237 no. 4, fq. 108–121, Bibcode:1977SciAm.237d.108A, doi:10.1038/scientificamerican1077-108 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Appel, Kenneth; Haken, Wolfgang (1989), Every Planar Map is Four-Colorable, Contemporary Mathematics, vëll. 98, With the collaboration of J. Koch., Providence, RI: American Mathematical Society, doi:10.1090/conm/098, ISBN 0-8218-5103-9, MR 1025335 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Bar-Natan, Dror (1997), "Lie algebras and the four color theorem", Combinatorica, 17 (1): 43–52, arXiv:q-alg/9606016, doi:10.1007/BF01196130, MR 1466574, S2CID 2103049 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Bernhart, Frank R. (1977), "A digest of the four color theorem", Journal of Graph Theory, vëll. 1 no. 3, fq. 207–225, doi:10.1002/jgt.3190010305, MR 0465921 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Borodin, O. V. (1984), "Solution of the Ringel problem on vertex-face coloring of planar graphs and coloring of 1-planar graphs", Metody Diskretnogo Analiza (41): 12–26, 108, MR 0832128 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!).
• Cayley, Arthur (1879), "On the colourings of maps", Proceedings of the Royal Geographical Society, Blackwell Publishing, 1 (4): 259–261, doi:10.2307/1799998, JSTOR 1799998 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Fritsch, Rudolf; Fritsch, Gerda (1998), The Four Color Theorem: History, Topological Foundations and Idea of Proof, Translated from the 1994 German original by Julie Peschke., New York: Springer, doi:10.1007/978-1-4612-1720-6, ISBN 978-0-387-98497-1, MR 1633950 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• F. G. (10 qershor 1854), "Tinting Maps", The Athenaeum: 726 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!).
• Gethner, E.; Springer, W. M. (2003), "How false is Kempe's proof of the four color theorem?", Congr. Numer, 164: 159–175, MR 2050581, Zbl 1050.05049 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Gethner, Ellen; Kalichanda, Bopanna; Mentis, Alexander S. (2009), "How false is Kempe's proof of the Four Color Theorem? Part II", Involve, 2 (3): 249–265, doi:10.2140/involve.2009.2.249 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Gonthier, Georges (2005), A computer-checked proof of the four colour theorem (PDF), unpublished {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Gonthier, Georges (2008), "Formal Proof—The Four-Color Theorem" (PDF), Notices of the American Mathematical Society, 55 (11): 1382–1393, MR 2463991 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Hadwiger, Hugo (1943), "Über eine Klassifikation der Streckenkomplexe", Vierteljschr. Naturforsch. Ges. Zürich, 88: 133–143 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Heawood, P. J. (1890), "Map-Colour Theorem", Quarterly Journal of Mathematics, Oxford, vëll. 24, fq. 332–338 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Hudson, Hud (maj 2003), "Four Colors Do Not Suffice", The American Mathematical Monthly, 110 (5): 417–423, doi:10.2307/3647828, JSTOR 3647828 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Kempe, A. B. (1879), "On the Geographical Problem of the Four Colours", American Journal of Mathematics, 2 (3): 193–220, doi:10.2307/2369235, JSTOR 2369235 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Magnant, C.; Martin, D. M. (2011), "Coloring rectangular blocks in 3-space", Discussiones Mathematicae Graph Theory, 31 (1): 161–170, doi:10.7151/dmgt.1535, arkivuar nga origjinali më 4 shkurt 2022, marrë më 4 shkurt 2022 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• McKay, Brendan D. (2012), A note on the history of the four-colour conjecture, arXiv:1201.2852, Bibcode:2012arXiv1201.2852M {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Nash-Williams, C. St. J. A. (1967), "Infinite graphs—a survey", Journal of Combinatorial Theory, 3 (3): 286–301, doi:10.1016/s0021-9800(67)80077-2, MR 0214501 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!).
• O'Connor; Robertson (1996), The Four Colour Theorem, MacTutor archive, arkivuar nga origjinali më 16 janar 2013, marrë më 4 shkurt 2022 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Pegg, Ed, Jr.; Melendez, J.; Berenguer, R.; Sendra, J. R.; Hernandez, A.; Del Pino, J. (2002), "Book Review: The Colossal Book of Mathematics" (PDF), Notices of the American Mathematical Society, 49 (9): 1084–1086, Bibcode:2002ITED...49.1084A, doi:10.1109/TED.2002.1003756 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)Mirëmbajtja CS1: Emra të shumëfishtë: lista e autorëve (lidhja)
• Reed, Bruce; Allwright, David (2008), "Painting the office", Mathematics-in-Industry Case Studies, 1: 1–8, arkivuar nga origjinali më 3 shkurt 2013, marrë më 4 shkurt 2022 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Ringel, G. (1974), Map Color Theorem, New York–Berlin: Springer-Verlag {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Ringel, G.; Youngs, J. W. T. (1968), "Solution of the Heawood Map-Coloring Problem", Proc. Natl. Acad. Sci. USA, vëll. 60 no. 2, fq. 438–445, Bibcode:1968PNAS...60..438R, doi:10.1073/pnas.60.2.438, PMC 225066, PMID 16591648 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Robertson, Neil; Sanders, Daniel P.; Seymour, Paul; Thomas, Robin (1996), "Efficiently four-coloring planar graphs", Proceedings of the 28th ACM Symposium on Theory of Computing (STOC 1996), fq. 571–575, doi:10.1145/237814.238005, MR 1427555, S2CID 14962541 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Robertson, Neil; Sanders, Daniel P.; Seymour, Paul; Thomas, Robin (1997), "The Four-Colour Theorem", J. Combin. Theory Ser. B, vëll. 70 no. 1, fq. 2–44, doi:10.1006/jctb.1997.1750, MR 1441258 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Saaty, Thomas; Kainen, Paul (1986), "The Four Color Problem: Assaults and Conquest", Science, New York: Dover Publications, 202 (4366): 424, Bibcode:1978Sci...202..424S, doi:10.1126/science.202.4366.424, ISBN 0-486-65092-8, PMID 17836752 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Swart, Edward Reinier (1980), "The philosophical implications of the four-color problem", American Mathematical Monthly, Mathematical Association of America, vëll. 87 no. 9, fq. 697–702, doi:10.2307/2321855, JSTOR 2321855, MR 0602826 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Thomas, Robin (1998), "An Update on the Four-Color Theorem" (PDF), Notices of the American Mathematical Society, vëll. 45 no. 7, fq. 848–859, MR 1633714 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Thomas, Robin (1995), The Four Color Theorem {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Tietze, Heinrich (1910), "Einige Bemerkungen zum Problem des Kartenfärbens auf einseitigen Flächen" [Some remarks on the problem of map coloring on one-sided surfaces], DMV Annual Report, 19: 155–159 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Thomas, Robin (1999), "Recent Excluded Minor Theorems for Graphs", përmbledhur nga Lamb, John D.; Preece, D. A. (red.), Surveys in combinatorics, 1999, London Mathematical Society Lecture Note Series, vëll. 267, Cambridge: Cambridge University Press, fq. 201–222, doi:10.1017/CBO9780511721335, ISBN 0-521-65376-2, MR 1725004 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Tait, P. G. (1880), "Remarks on the colourings of maps", Proc. R. Soc. Edinburgh, 10: 729, doi:10.1017/S0370164600044643 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)
• Wilson, Robin (2014) [2002], Four Colors Suffice, Princeton Science Library, Princeton, NJ: Princeton University Press, ISBN 978-0-691-15822-8, MR 3235839 {{citation}}: Mungon ose është bosh parametri |language= (Ndihmë!)

Linqe te jashtme ==

• "Four-colour problem", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Weisstein, Eric W. "Blanuša snarks". MathWorld.
• Weisstein, Eric W. "Map coloring". MathWorld.
• List of generalizations of the four color theorem on MathOverflow