Funksioni i gabimit

Në matematikë, funksioni i gabimit (i quajtur edhe funksioni i gabimit të Gausit ), i shënuar shpesh me erf, është një funksion kompleks i një ndryshoreje komplekse të përcaktuar si: [1]
Disa autorë përcaktojnë pa faktorin . [2] Ky integral jo-elementar është një funksion sigmoid që haset shpesh në probabilitet, statistikë dhe ekuacione diferenciale të pjesshme . Në shumë prej këtyre zbatimeve, argumenti i funksionit është një numër real. Nëse argumenti i funksionit është real, atëherë vlera e funksionit është gjithashtu reale.
Në statistika, për vlerat jonegative të , funksioni i gabimit ka interpretimin e mëposhtëm: për një ndryshore të rastësishme që shpërndahet normalisht me mesatare 0 dhe shmangie standarde , është probabiliteti që të jetë në segmentin .
Dy funksione të lidhura ngushtë janë funksioni i gabimit plotësues ( erfc ) i përcaktuar si
dhe funksioni i gabimit imagjinar ( erfi ) i përcaktuar si
ku i është njësia imagjinare .
Emri[Redakto | Redakto nëpërmjet kodit]
Emri "funksioni i gabimit" dhe shkurtesa e tij erf u propozuan nga JWL Glaisher në 1871 për shkak të lidhjes së tij me "teorinë e probabilitetit, dhe veçanërisht teorinë e gabimeve ". [3] Plotësi i funksionit të gabimit u diskutua gjithashtu nga Glaisher në një botim të veçantë në të njëjtin vit. [4] Për "ligjin e lehtësirave" të gabimeve dendësia e të cilave jepet nga
( shpërndarja normale ), Glaisher llogarit probabilitetin e një gabimi që shtrihet midis p dhe q si:
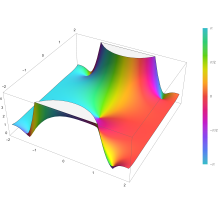
Vizatimi i funksionit të gabimit Erf(z) në planin kompleks nga në me ngjyra të krijuara me funksionin Mathematica 13.1 ComplexPlot3D
Zbatimet[Redakto | Redakto nëpërmjet kodit]
Kur rezultatet e një serie matjesh përshkruhen nga një shpërndarje normale me shmangie standarde dhe pritje matematike 0, atëherë është probabiliteti që gabimi i një matje të vetme të shtrihet mes dhe për pozitive. Kjo është e dorës për shëmbull kur përcaktohet shkalla e gabimit të biteve në një sistem dixhital komunikimi.
Funksionet e gabimit dhe gabimit plotësues ndodhin, për shembull, në zgjidhjet e ekuacionit të nxehtësisë kur kushtet kufitare jepen nga funksioni i hapit Heaviside .
Funksioni i gabimit dhe përafrimet e tij mund të përdoren për të vlerësuar rezultate që qëndrojnë me probabilitet të lartë ose me probabilitet të ulët. Jepet një ndryshore e rastit (një shpërndarje normale me mesatare μ dhe devijim standard σ ) dhe një konstante :
ku A dhe B janë konstante numerike të caktuara. Nëse L është mjaftueshëm larg nga mesatarja, konkretisht atëherë:
pra probabiliteti shkon në 0 kur k → ∞ .
Probabiliteti që të jetë në intervalin mund të nxirret si
Vetitë[Redakto | Redakto nëpërmjet kodit]
Vetia do të thotë që funksioni i gabimit është një funksion tek . Kjo rezulton drejtpërdrejt nga fakti se i integrueshmi është një funksion çift (integrali i pacaktuar i një funksioni çift që është zero në origjinë është një funksion tek dhe anasjelltas).
Meqenëse funksioni i gabimit është një funksion i tërë që merr numrat realë në numra realë, për çdo numër kompleks :
ku z është i konjuguari kompleks i .
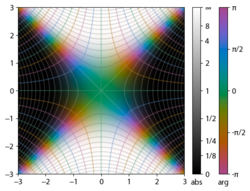
I integrueshmi dhe janë paraqitur në planin kompleks z në figurat djathtas me ngjyrosjen e domenit .
Funksioni i gabimit në +∞ është saktësisht 1 (shih integralin Gaussian ). Në boshtin real, i afrohet unitetit në z → +∞ dhe −1 në z → −∞ . Në boshtin imagjinar, tenton drejt ±i ∞ .
Seria e Tejlorit[Redakto | Redakto nëpërmjet kodit]
Funksioni i gabimit është një funksion i tërë ; ai nuk ka pika dyshimi (përveç asaj në pafundësi) dhe zgjerimi i tij Tejlor konvergjon gjithmonë, por është i njohur në mënyrë të famshme "[...] për konvergjencën e tij të keqe nëse ." [5]
Integrali përcaktues nuk mund të vlerësohet në formë të mbyllur për sa i përket funksioneve elementare (shih teoremën e Liouville ), por duke zgjeruar integrandin në serinë e tij Meklauren dhe duke integruar term pas termi, fitohet seria Meklauren e funksionit të gabimit si:
që vlen për çdo numër kompleks z . Termat e emëruesit janë seria A007680 në OEIS .
Për llogaritjen iterative të serisë së mësipërme, formulimi alternativ i mëposhtëm mund të jetë i dobishëm:
Funksioni i gabimit imagjinar ka një seri shumë të ngjashme Meklauren, e cila është:
që vlen për çdo numër kompleks z .
Derivati dhe integrali[Redakto | Redakto nëpërmjet kodit]
Derivati i funksionit të gabimit rrjedh menjëherë nga përkufizimi i tij:
Nga kjo, derivati i funksionit të gabimit imagjinar është gjithashtu i menjëhershëm:
Një antiderivativ i funksionit të gabimit, që arrihet nga integrimi me pjesë, është
Një antiderivativ i funksionit të gabimit imagjinar, që arrihet gjithashtu nga integrimi me pjesë, është
Derivatet e rendeve të larta jepen nga
Tabela e vlerave[Redakto | Redakto nëpërmjet kodit]
| x | erf x | 1 − erf x |
|---|---|---|
| 0 | 0 | 1 |
| 0.02 | 0.022564575 | 0.977435425 |
| 0.04 | 0.045111106 | 0.954888894 |
| 0.06 | 0.067621594 | 0.932378406 |
| 0.08 | 0.090078126 | 0.909921874 |
| 0.1 | 0.112462916 | 0.887537084 |
| 0.2 | 0.222702589 | 0.777297411 |
| 0.3 | 0.328626759 | 0.671373241 |
| 0.4 | 0.428392355 | 0.571607645 |
| 0.5 | 0.520499878 | 0.479500122 |
| 0.6 | 0.603856091 | 0.396143909 |
| 0.7 | 0.677801194 | 0.322198806 |
| 0.8 | 0.742100965 | 0.257899035 |
| 0.9 | 0.796908212 | 0.203091788 |
| 1 | 0.842700793 | 0.157299207 |
| 1.1 | 0.880205070 | 0.119794930 |
| 1.2 | 0.910313978 | 0.089686022 |
| 1.3 | 0.934007945 | 0.065992055 |
| 1.4 | 0.952285120 | 0.047714880 |
| 1.5 | 0.966105146 | 0.033894854 |
| 1.6 | 0.976348383 | 0.023651617 |
| 1.7 | 0.983790459 | 0.016209541 |
| 1.8 | 0.989090502 | 0.010909498 |
| 1.9 | 0.992790429 | 0.007209571 |
| 2 | 0.995322265 | 0.004677735 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0.001862846 |
| 2.3 | 0.998856823 | 0.001143177 |
| 2.4 | 0.999311486 | 0.000688514 |
| 2.5 | 0.999593048 | 0.000406952 |
| 3 | 0.999977910 | 0.000022090 |
| 3.5 | 0.999999257 | 0.000000743 |
- ^ Andrews, Larry C. (1998). Special functions of mathematics for engineers. SPIE Press. fq. 110. ISBN 9780819426161.
{{cite book}}: Mungon ose është bosh parametri|language=(Ndihmë!) - ^ Whittaker, E. T.; Watson, G. N. (1927). A Course of Modern Analysis. Cambridge University Press. fq. 341. ISBN 978-0-521-58807-2.
{{cite book}}: Mungon ose është bosh parametri|language=(Ndihmë!) - ^ Glaisher, James Whitbread Lee (korrik 1871). "On a class of definite integrals". London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42: 294–302. doi:10.1080/14786447108640568. Marrë më 6 dhjetor 2017.
{{cite journal}}: Mungon ose është bosh parametri|language=(Ndihmë!) - ^ Glaisher, James Whitbread Lee (shtator 1871). "On a class of definite integrals. Part II". London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42: 421–436. doi:10.1080/14786447108640600. Marrë më 6 dhjetor 2017.
{{cite journal}}: Mungon ose është bosh parametri|language=(Ndihmë!) - ^ "A007680 – OEIS". oeis.org. Marrë më 2020-04-02.
{{cite web}}: Mungon ose është bosh parametri|language=(Ndihmë!)








![{\displaystyle [-x,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e23c41ff0bd6f01a0e27054c2b85819fcd08b762)













![{\displaystyle {\begin{aligned}\Pr[X\leq L]&={\frac {1}{2}}+{\frac {1}{2}}\operatorname {erf} {\frac {L-\mu }{{\sqrt {2}}\sigma }}\\&\approx A\exp \left(-B\left({\frac {L-\mu }{\sigma }}\right)^{2}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3cb760eaf336393db9fd0bb12c4465655a27de8)

![{\displaystyle \Pr[X\leq L]\leq A\exp(-B\ln {k})={\frac {A}{k^{B}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2baadea015e20a45d1034fd88eed861e7fcce178)

![{\displaystyle [L_{a},L_{b}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58207aec00d8beddde120e1a97cfb5fde7d9be0a)
![{\displaystyle {\begin{aligned}\Pr[L_{a}\leq X\leq L_{b}]&=\int _{L_{a}}^{L_{b}}{\frac {1}{{\sqrt {2\pi }}\sigma }}\exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)\,\mathrm {d} x\\&={\frac {1}{2}}\left(\operatorname {erf} {\frac {L_{b}-\mu }{{\sqrt {2}}\sigma }}-\operatorname {erf} {\frac {L_{a}-\mu }{{\sqrt {2}}\sigma }}\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd2214f0db2c1d36075815825b616501175c6283)










![{\displaystyle {\begin{aligned}\operatorname {erf} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{n!(2n+1)}}\\[6pt]&={\frac {2}{\sqrt {\pi }}}\left(z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{10}}-{\frac {z^{7}}{42}}+{\frac {z^{9}}{216}}-\cdots \right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c80541f305af070bb0510625c584fe1559a0cd2c)
![{\displaystyle {\begin{aligned}\operatorname {erf} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }\left(z\prod _{k=1}^{n}{\frac {-(2k-1)z^{2}}{k(2k+1)}}\right)\\[6pt]&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z}{2n+1}}\prod _{k=1}^{n}{\frac {-z^{2}}{k}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dca22e8e7dee0297e87a455249c282c6b92fedcb)
![{\displaystyle {\begin{aligned}\operatorname {erfi} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z^{2n+1}}{n!(2n+1)}}\\[6pt]&={\frac {2}{\sqrt {\pi }}}\left(z+{\frac {z^{3}}{3}}+{\frac {z^{5}}{10}}+{\frac {z^{7}}{42}}+{\frac {z^{9}}{216}}+\cdots \right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ff91095cd6825137cc951ec0a786db0b7f68fac)




