Rrethi njësi

Ilustrimi i një rrethi njësi. Ndryshorja t është një masë këndi .

Animacion i aktit të zbërthimit të perimetrit të një rrethi njësi, një rrethi me rreze 1. Meqenëse C = 2 πr, perimetri i një rrethi njësi është 2π .

Në matematikë, një rreth njësi është një rreth me rreze njësi - domethënë një rreze prej 1 njësie. Shpesh, veçanërisht në trigonometri, rrethi i njësisë është rrethi i rrezes 1 me qendër në origjinën (0, 0) në sistemin e koordinatave karteziane në rrafshin Euklidian. Në topologji, shpesh shënohet si S¹ sepse është një njësi njëdimensionale sferë - n .

Nëse (x, y) është një pikë në perimetrin e rrethit njësi, atëherë |x| dhe |y| janë gjatësitë e këmbëve të një trekëndëshi kënddrejtë, hipotenuza e të cilit ka gjatësi 1. Kështu, nga teorema e Pitagorës, x dhe y plotësojnë ekuacionin $$x^{2}+y^{2}=1.$$

Meqenëse x² = (−x)² për të gjitha x, dhe meqenëse pasqyrimi i çdo pike në rrethin e njësisë rreth boshtit x - ose y është gjithashtu në rrethin njësi, ekuacioni i mësipërm vlen për të gjitha pikat (x, y) në rrethin e njësisë, jo vetëm ato në kuadrantin e parë.

Pjesa e brendshme e rrethit të njësisë quhet disku i njësisë së hapur, ndërsa pjesa e brendshme e rrethit të njësisë e kombinuar me vetë rrethin e njësisë quhet disku i njësisë së mbyllur.

Në planin kompleks

Animimi i rrethit njësi me kënde

Në rrafshin kompleks, numrat e madhësisë njësi quhen numra kompleks njësi . Ky është bashkësia e numrave kompleksë z të tillë që $|z|=1.$ Kur ndahet në përbërës realë dhe imagjinarë $z=x+iy,$ kjo gjendje është $|z|^{2}=z{\bar {z}}=x^{2}+y^{2}=1.$

Rrethi kompleks i njësisë mund të parametrizohet me masë këndi $\theta$ nga boshti real pozitiv duke përdorur funksionin kompleks eksponencial, $z=e^{i\theta }=\cos \theta +i\sin \theta .$

Funksionet trigonometrike në rrethin njësi

Të gjitha funksionet trigonometrike të këndit θ (theta) mund të ndërtohen gjeometrikisht në terma të një rrethi njësi të përqendruar në O.

Funksioni i sinusit në rrethin e njësisë (lart) dhe grafiku i tij (poshtë)

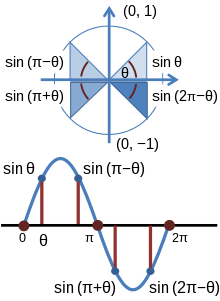
Funksionet trigonometrike kosinus dhe sinus të këndit θ mund të përcaktohen në rrethin njësi si më poshtë: Nëse (x, y ) është një pikë në rrethin njësi, dhe nëse rrezja nga origjina (0, 0) në (x, y ) formon një kënd θ nga boshti pozitiv x, (ku kthimi në drejtim të kundërt të akrepave të orës është pozitiv), atëherë $$\cos \theta =x\quad {\text{and}}\quad \sin \theta =y.$$

Ekuacioni x² + y² = 1 jep relacionin $$\cos ^{2}\theta +\sin ^{2}\theta =1.$$

Rrethi i njësisë tregon gjithashtu se sinusi dhe kosinusi janë funksione periodike, me identitetet $$\cos \theta =\cos(2\pi k+\theta )$$$$\sin \theta =\sin(2\pi k+\theta )$$ për çdo numër të plotë k .

Duke përdorur rrethin e njësisë, vlerat e çdo funksioni trigonometrik për shumë kënde të ndryshme nga ato të etiketuara mund të llogariten lehtësisht me dorë duke përdorur formulat e shumës dhe ndryshesës së këndeve .

Rrethi njësi, që tregon koordinatat e pikave të caktuara

Dinamika komplekse

Rrethi njësi në dinamikë komplekse

Bashkësia Julia e sistemit dinamik jolinear diskret me funksion evolucioni : $$f_{0}(x)=x^{2}$$ është një rreth njësi. Është një rast më i thjeshtë, kështu që përdoret gjerësisht në studimin e sistemeve dinamike.