Hapësira vektoriale

Mbledhja e vektorëve dhe shumëzimi skalar: një vektor v (blu) i shtohet një vektori tjetër (i kuq, ilustrimi i sipërm). Më poshtë, w shtrihet me një faktor 2, duke dhënë shumën v + 2 w .

Në matematikë dhe fizikë, një hapësirë vektoriale (e quajtur edhe hapësirë lineare ) është një grup elementët e të cilit, shpesh të quajtur vektorë, mund të mblidhen së bashku dhe të shumëzohen ("shkallëzohen") me numra të quajtur skalarë. Skalarët janë shpesh numra realë, por mund të jenë numra kompleksë ose, në përgjithësi, elemente të çdo fushe. Veprimet e mbledhjes së vektorit dhe shumëzimit skalar duhet të plotësojnë disa kërkesa, të quajtura aksioma vektoriale. Termat hapësirë vektoriale reale dhe hapësirë vektoriale komplekse përdoren shpesh për të specifikuar natyrën e skalarëve: hapësirë koordinative reale ose hapësirë koordinative komplekse .

Hapësirat vektoriale përgjithësojnë vektorët Euklidianë, të cilët lejojnë modelimin e madhësive fizike, si forca dhe shpejtësia, që kanë jo vetëm madhësi, por edhe drejtim e kah. Koncepti i hapësirave vektoriale është themelor për algjebrën lineare, së bashku me konceptin e matricave, të cilat lejojnë llogaritjet në hapësirat vektoriale. Kjo siguron një mënyrë të saktë dhe koncize për manipulimin dhe studimin e sistemeve të ekuacioneve lineare .

Hapësirat vektoriale karakterizohen nga dimensioni i tyre, i cili, përafërsisht, specifikon numrin e drejtimeve të pavarura në hapësirë. Kjo do të thotë se, për dy hapësira vektoriale mbi një fushë të caktuar dhe me të njëjtin dimension, vetitë që varen vetëm nga struktura e hapësirës janë të njëjta (teknikisht hapësirat vektoriale janë izomorfe ). Një hapësirë vektoriale është me dimensione të fundme nëse dimensioni i saj është një numër natyror . Përndryshe, ai është me dimensione të pafundme, dhe dimensioni i tij është një kardinal i pafundëm . Hapësirat vektoriale me dimensione të fundme ndodhin natyrshëm në gjeometri dhe zona të lidhura me to. Hapësirat vektoriale me dimensione të pafundme hasen në shumë fusha të matematikës. Për shembull, unazat polinomiale janë hapësira vektoriale me dimensione të pafundme të numërueshme dhe shumë hapësira funksionesh kanë si dimension kardinalitetin e vazhdimësisë .

Shumë hapësira vektoriale që studiohen në matematikë janë të pajisura edhe me struktura të tjera. Ky është rasti i algjebrave, të cilat përfshijnë zgjerimet e fushës, unazat polinomiale, algjebrat shoqëruese dhe algjebrat Lie . Ky është gjithashtu rasti i hapësirave vektoriale topologjike, të cilat përfshijnë hapësirat funksionale, hapësirat e produkitit të brëndshëm, hapësirat e normuara, hapësirat Hilbert dhe hapësirat Banach .

Përkufizimi dhe vetitë themelore

Në këtë artikull, vektorët janë paraqitur përgjithësisht me shkronja të zeza për t'i dalluar ata nga skalarët.

Një hapësirë vektoriale mbi një fushë F është një grup jo bosh V së bashku me dy veprime binare që plotësojnë tetë aksiomat e renditura më poshtë. Në këtë kontekst, elementët e V quhen zakonisht vektorë, dhe elementët e F quhen skalarë .

• Veprimi i parë, i quajtur shtim vektori ose thjesht shtim, i cakton çdo dy vektori v dhe w në V një vektor i tretë në V i cili zakonisht shkruhet si v + w dhe quhet shuma e këtyre dy vektorëve.
• Veprimi i dytë, i quajtur shumëzim skalar, i cakton çdo skalari a në F dhe çdo vektor v në V një vektor tjetër në V, i cili shënohet a v .

Për të pasur një hapësirë vektoriale, tetë aksiomat e mëposhtme duhet të plotësohen për çdo u, v dhe w në V, dhe a dhe b në F .

Aksiomë	Kuptimi
Vetia shoqëruese e mbledhjes së vektorit	u + ( v + w ) = ( u + v ) + w
Vetia ndërruese i mbledhjes së vektorit	u + v = v + u
Elementi i identitetit të mbledhjes së vektorit	Ekziston një element 0 ∈ V, i quajtur vektori zero, i tillë që v + 0 = v për të gjithë v ∈ V .
Elementet e anasjellta të mbledhjes së vektorit	Për çdo v ∈ V, ekziston një element −v ∈ V, i quajtur mbledhës i kundërt i v, i tillë që v + (− v ) = 0 .
Pajtueshmëria e shumëzimit skalar me shumëzimin e fushës	a ( b v ) = ( ab ) v
Elementi i identitetit të shumëzimit skalar	1v= v, ku 1 tregon identitetin shumëzues në F
Përdasia e shumëzimit skalar në lidhje me mbledhjen e vektorit	a ( u + v ) = a u + a v
Shpërndarja e shumëzimit skalar në lidhje me mbledhjen e fushës	(a + b ) v = a v + b v

Kur fusha skalare është numrat realë, hapësira vektoriale quhet hapësirë vektoriale reale . Kur fusha skalare është numrat komplekse, hapësira vektoriale quhet hapësirë vektoriale komplekse . Këto dy raste janë më të zakonshmet, por zakonisht merren parasysh edhe hapësirat vektoriale me skalorë në një fushë arbitrare F. Një hapësirë e tillë vektoriale quhet një hapësirë F - vektoriale ose një hapësirë vektoriale mbi F

Zbritja e dy vektorëve mund të përkufizohet si$$\mathbf {v} -\mathbf {w} =\mathbf {v} +(-\mathbf {w} ).$$Pasojat e drejtpërdrejta të aksiomave përfshijnë se për çdo $s\in F$ dhe $\mathbf {v} \in V,$ marrim këto identitete

• $0\mathbf {v} =\mathbf {0} ,$
• $s\mathbf {0} =\mathbf {0} ,$
• $(-1)\mathbf {v} =-\mathbf {v} ,$
• $s\mathbf {v} =\mathbf {0}$ nënkupton $s=0$ ose $\mathbf {v} =\mathbf {0} .$

Konceptet dhe vetitë e ndërlidhura

Një vektor v në R 2 (blu) i shprehur në terma të bazave të ndryshme: duke përdorur bazën standarde në R² : v = xe₁ + ye₂ (e zezë), dhe duke përdorur një bazë të ndryshme, jo- ortogonale : v = f₁+ f₂ (e kuqe).

Kombinim linear

Duke pasur parasysh një bashkësi elementësh G të një hapësire F -vektoriale V, një kombinim linear i elementeve të G është një element i V i formës$$a_{1}\mathbf {g} _{1}+a_{2}\mathbf {g} _{2}+\cdots +a_{k}\mathbf {g} _{k},$$$a_{1}\mathbf {g} _{1}+a_{2}\mathbf {g} _{2}+\cdots +a_{k}\mathbf {g} _{k},$

$$a_{1}\mathbf {g} _{1}+a_{2}\mathbf {g} _{2}+\cdots +a_{k}\mathbf {g} _{k},$$

Pavarësia lineare

Elementet e një nënbashkësie G të një hapësire F -vektoriale V thuhet se janë linearisht të pavarur nëse asnjë element i G nuk mund të shkruhet si një kombinim linear i elementeve të tjerë të G . Në mënyrë ekuivalente, ato janë linearisht të pavarura nëse dy kombinime lineare të elementeve të G përcaktojnë të njëjtin element të V nëse dhe vetëm nëse kanë të njëjtët koeficientë.

Nënhapësirë lineare

Një nënhapësirë lineare ose nënhapësirë vektoriale W e një hapësire vektoriale V është një nënbashkësi joboshe i V që mbyllet nën mbledhjen e vektorit dhe shumëzimin skalar; domethënë, shuma e dy elementeve të W dhe prodhimi i një elementi të V me një skalar i përkasin W. Kjo nënkupton që çdo kombinim linear i elementeve të W i përket W.


Vetia e mbylljes nënkupton gjithashtu se çdo kryqëzim i nënhapësirave lineare është një nënhapësirë lineare.

Spani linear

Duke pasur parasysh një nënbashkësi G të një hapësire vektoriale V, hapësira lineare ose thjesht hapësira e G është nënhapësira lineare më e vogël e V që përmban G, në kuptimin që është kryqëzimi i të gjitha nënhapësirave lineare që përmbajnë G . Hapësira e G është gjithashtu bashkësia e të gjitha kombinimeve lineare të elementeve të G .



Nëse W është hapësira e G, dikush thotë se G përfshin ose gjeneron W, dhe se G është një bashkësi shtrirëse ose një bashkësia gjeneruese e W .

Baza dhe dimensioni

Një nënbashkësi e një hapësire vektoriale është një bazë nëse elementet e saj janë linearisht të pavarur dhe shtrihen në hapësirën vektoriale. Çdo hapësirë vektoriale ka të paktën një bazë, përgjithësisht shumë. Për më tepër, të gjitha bazat e një hapësire vektoriale kanë të njëjtin kardinalitet, i cili quhet dimensioni i hapësirës vektoriale (shih teoremën e dimensionit për hapësirat vektoriale ).

Shembuj

Shigjeta në një plan

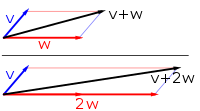
Shembulli i parë i një hapësire vektoriale përbëhet nga shigjeta në një plan të fiksuar, duke filluar nga një pikë. Kjo përdoret në fizikë për të përshkruar forcat ose shpejtësitë . Duke pasur parasysh çdo dy shigjeta të tilla, v dhe w, paralelogrami i shtrirë nga këto dy shigjeta përmban një shigjetë diagonale që fillon gjithashtu nga origjina. Kjo shigjetë e re quhet shuma e dy shigjetave dhe shënohet v + w . Në rastin e veçantë të dy shigjetave në të njëjtën vijë, shuma e tyre është shigjeta në këtë vijë, gjatësia e së cilës është shuma ose ndryshimi i gjatësive, nëse shigjetat kanë të njëjtin drejtim apo jo. Një veprim tjetër që mund të bëhet me shigjeta është shkallëzimi: duke pasur parasysh çdo numër real pozitiv a, shigjeta që ka të njëjtin drejtim si v, por zgjerohet ose zvogëlohet duke shumëzuar gjatësinë e saj me a, quhet shumëzim i v me a . Është shënuar av . Kur a është negative, a v përcaktohet si shigjeta që tregon në drejtim të kundërt.

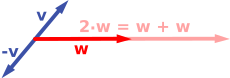
Shembulli i dytë: çiftet e renditura të numrave

Një shembull i dytë kyç i një hapësire vektoriale sigurohet nga çiftet e numrave realë x dhe y . (Rendi i përbërësve x dhe y është i rëndësishëm, kështu që një çift i tillë quhet edhe çift i renditur . ) Një çift i tillë shkruhet si (x, y ) . Shuma e dy çifteve të tilla dhe shumëzimi i një çifti me një numër përcaktohet si më poshtë:$$(x_{1},y_{1})+(x_{2},y_{2})=(x_{1}+x_{2},y_{1}+y_{2})$$dhe$$a(x,y)=(ax,ay).$$

Numrat kompleks dhe zgjerimet e tjera të fushave

Bashkësia e numrave kompleksë C, pra numrat që mund të shkruhen në formën x + iy për numrat realë x dhe y ku i është njësia imagjinare, formojnë një (x + iy) + (a + ib)= (x + a)+ i( y + b) dhe gjithashtu shumëzimi skalar c ⋅ (x + iy) = (c ⋅ x) + i(c ⋅ y) për numrat realë x, y, a, b dhe c .

Hapësirat funksionale

Mbledhja e funksioneve: shuma e sinusit dhe funksionit eksponencial është $\sin +\exp :\mathbb {R} \to \mathbb {R}$ me $(\sin +\exp )(x)=\sin(x)+\exp(x)$ .

Funksionet nga çdo bashkësi fikse Ω në një fushë F gjithashtu formojnë hapësira vektoriale, duke kryer mbledhjen dhe shumëzimin skalar për çdo pikë. Kjo do të thotë se shuma e dy funksioneve f dhe g është funksioni $(f+g)$ dhënë nga$$(f+g)(w)=f(w)+g(w),$$dhe në mënyrë të ngjashme për shumëzimin. Hapësira të tilla funksionale hasen në shumë situata gjeometrike, kur Ω është vija reale ose një interval, ose nënbashkësi të tjera të R . Shumë nocione në topologji dhe analizë matematike, të tilla si vazhdimësia, integrueshmëria ose diferencueshmëria janë të mirësjellura në lidhje me linearitetin: shumat dhe shumëfishat skalorë të funksioneve që zotërojnë një veti të tillë ende e kanë atë veti. Prandaj, grupi i funksioneve të tilla janë hapësira vektoriale, studimi i të cilave i përket analizës funksionale .

Ekuacionet lineare

Sistemet e ekuacioneve lineare homogjene janë të lidhura ngushtë me hapësirat vektoriale. Për shembull, zgjidhjet e$${\begin{alignedat}{9}&&a\,&&+\,3b\,&\,+&\,&c&\,=0\\4&&a\,&&+\,2b\,&\,+&\,2&c&\,=0\\\end{alignedat}}$$jepen me treshe arbitrare sipas koeficientëve $a,$$b=a/2,$ dhe $c=-5a/2.$ Ato formojnë një hapësirë vektoriale: shumat dhe shumëfishat skalorë të treshave të tillë ende plotësojnë të njëjtat raporte të tre variablave; kështu që edhe ato janë zgjidhje. Matricat mund të përdoren për të kondensuar ekuacionet e shumta lineare si më sipër në një ekuacion vektorial, përkatësisht

$$A\mathbf {x} =\mathbf {0} ,$$

ku $A={\begin{bmatrix}1&3&1\\4&2&2\end{bmatrix}}$ është matrica që përmban koeficientët e ekuacioneve të dhëna, $\mathbf {x}$ është vektori $(a,b,c),$$A\mathbf {x}$ tregon prodhimin e matricës dhe $\mathbf {0} =(0,0)$ është vektori zero. Në një mënyrë të ngjashme, zgjidhjet e ekuacioneve diferenciale lineare homogjene formojnë hapësira vektoriale. Për shembull,

$$f^{\prime \prime }(x)+2f^{\prime }(x)+f(x)=0$$

jep zgjidhjen $f(x)=ae^{-x}+bxe^{-x},$ ku $a$ dhe $b$ janë konstante arbitrare, dhe $e^{x}$ është funksioni natyror eksponencial .

Hartat lineare dhe matricat

Lidhja e dy hapësirave vektoriale mund të shprehet me hartë lineare ose transformim linear . Ato janë funksione që pasqyrojnë strukturën e hapësirës vektoriale, domethënë ruajnë veprimet e mbledhjes dhe shumëzimin skalar:$$f(\mathbf {v} +\mathbf {w} )=f(\mathbf {v} )+f(\mathbf {w} ),{\text{ and }}$$$$f(a\cdot \mathbf {v} )=a\cdot f(\mathbf {v} )$$per te gjithe $\mathbf {v}$ dhe $\mathbf {w}$ në $V,$ të gjitha $a$ në $F.$

Një izomorfizëm është një hartë lineare f : V → W e tillë që ekziston një hartë e anasjelltë g : W → V, e cila është një hartë e tillë që dy kompozimet e mundshme f ∘ g : W → W dhe g ∘ f : V → V janë harta identiteti . Në mënyrë të njëvlershme, f është edhe një-me-një ( injektiv ) dhe mbi ( syrjektiv ). Nëse ekziston një izomorfizëm midis V dhe W, të dy hapësirat thuhet se janë izomorfe ; atëherë ato janë në thelb identike si hapësira vektoriale, pasi të gjitha identitetet që mbahen në V transportohen, nëpërmjet f, në ato të ngjashme në W, dhe anasjelltas nëpërmjet g .

Matricat

Një matricë tipike

Matricat janë një nocion i dobishëm për të koduar hartat lineare. Ato shënohen si një grup drejtkëndor skalarësh si në imazhin në të djathtë. Çdo matricë m -nga- n $A$ krijon një hartë lineare nga F n në F m, nga sa vijon$$\mathbf {x} =(x_{1},x_{2},\ldots ,x_{n})\mapsto \left(\sum _{j=1}^{n}a_{1j}x_{j},\sum _{j=1}^{n}a_{2j}x_{j},\ldots ,\sum _{j=1}^{n}a_{mj}x_{j}\right),$$ku $\sum$ tregon mbledhjen, ose, duke përdorur shumëzimin e matricës së matricës $A$ me vektorin e koordinatave $\mathbf {x} :$

$$\mathbf {x} \mapsto A\mathbf {x} .$$

Për më tepër, pas zgjedhjes së bazave të V dhe W, çdo hartë lineare f : V → W përfaqësohet në mënyrë unike nga një matricë nëpërmjet kësaj caktimi.

Përcaktori det (A) i një matrice katrore A është një skalar që tregon nëse harta shoqëruese është një izomorfizëm apo jo: për të qenë e tillë është e mjaftueshme dhe e nevojshme që përcaktori të jetë jozero. Transformimi linear i Rⁿ që i përkon matricës reale me përmasa n x n e ruan orientimin atëherë dhe vetëm atëherë nëse përcaktori i tij është pozitiv.

Eigenvlerat dhe eigenvektorët

Endomorfizmat, harta lineare f : V → V, janë veçanërisht të rëndësishme pasi në këtë rast vektorët v mund të krahasohen me imazhin e tyre nën funksionin f, f(v) . Çdo vektor jozero v që kënaq λv = f(v) , ku λ është skalar, quhet eigenvektor i f me eigenvlerë λ . Në mënyrë të njëvlerëshme, v është një element i bërthamës i ndryshesës f − λ · Id (ku Id është hartëzimi identik V → V ) . Nëse V është me dimensione të fundme, kjo mund të riformulohet duke përdorur përcaktorë: f që ka vlerën vetjake λ është ekuivalente me$$\det(f-\lambda \cdot \operatorname {Id} )=0.$$