Këndi i ngurtë

Këndi i ngurtë
Këndi i ngurtë
Simbole të zakonshme	Ω
Njësitë SI	steradian
Njësi të tjera	Gradë në katror
Në njësitë bazë SI	m2/m2
Conserved	No
Derivimi nga ekuacione të tjera
Dimensioni

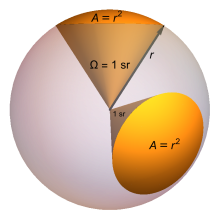
$\Omega ={\frac {A}{r^{2}}},$ Në gjeometri, një kënd i ngurtë (simboli: Ω ) është një masë e sasisë së fushës së shikimit nga një pikë e veçantë që mbulon një objekt i caktuar. Kjo do të thotë se është një masë se sa i madh i duket objekti një vëzhguesi që shikon nga ajo pikë. Pika nga e cila shikohet objekti quhet kulmi i këndit të ngurtë, dhe objekti thuhet se tendos këndin e tij të ngurtë në atë pikë.

Në Sistemin Ndërkombëtar të Njësive (SI), një kënd i ngurtë shprehet në një njësi pa dimension të quajtur steradian (simbol: sr). Një steradian përkon me një njësi të sipërfaqes në sferën njësi që rrethon kulmin, kështu që një objekt që bllokon të gjitha rrezet nga kulmi do të mbulonte një numër steradianësh të barabartë me sipërfaqen totale të sferës njësi, $4\pi$ .

Një objekt i vogël afër mund të tendosë të njëjtin kënd të ngurtë si një objekt më i madh më larg. Për shembull, megjithëse Hëna është shumë më e vogël se Dielli, ajo është gjithashtu shumë më afër Tokës . Në të vërtetë, siç shihet nga çdo pikë në Tokë, të dy objektet kanë afërsisht të njëjtin kënd të ngurtë (dhe për rrjedhojë madhësinë e dukshme). Kjo është e dukshme gjatë një eklipsi diellor .

Përkufizimi dhe vetitë

Këndi i ngurtë i një objekti në steradianë është i barabartë me sipërfaqen e segmentit të një sfere njësi, e qëndërzuar në apeks, që mbulon objekti. Dhënia e sipërfaqes së një segmenti të një sfere njësi në steradianë është analoge me dhënien e gjatësisë së një harku të një rrethi njësi në radianë. Ashtu si një kënd i rrafshët në radianë është raporti i gjatësisë së një harku me rrezen e tij, një kënd i ngurtë në steradianë është raporti i sipërfaqes së mbuluar në një sferë nga një objekt me sipërfaqen e dhënë nga katrori i rrezes së sferës në fjalë. Formula është

ku $A$ është sipërfaqja sferike dhe $r$ është rrezja e sferës së konsideruar.

Këndet e ngurta përdoren shpesh në astronomi, fizikë dhe në veçanti në astrofizikë . Këndi i ngurtë i një objekti që është shumë larg është afërsisht përpjestimor me raportin e sipërfaqes me largësinë në katror. Këtu "zona" nënkupton zonën e objektit kur projektohet përgjatë drejtimit të shikimit.

Këndi i ngurtë i një sfere i matur nga çdo pikë në brendësi të saj është 4 π sr, dhe këndi i ngurtë i vendosur në qendër të një kubi nga një nga faqet e tij është një e gjashta e tij, ose 2 π /3 sr. Këndet e ngurta mund të maten gjithashtu në gradë katrore (1 sr = ( ² gradë katrore), në arkminuta katror dhe në arksekonda katror.

Në koordinatat sferike ekziston një formulë për diferencialin , $d\Omega =\sin \theta \,d\theta \,d\varphi ,$ ku θ është bashkëgjatësia (këndi nga Poli i Veriut) dhe φ është gjatësia.

Këndi i ngurtë për një sipërfaqe të orientuar arbitrare S të tendosur në një pikë P është e barabartë me këndin e ngurtë të projeksionit të sipërfaqes S në sferën e njësisë me qendër P, e cila mund të llogaritet si integrali sipërfaqësor : $\Omega =\iint _{S}{\frac {{\hat {r}}\cdot {\hat {n}}}{r^{2}}}\,dS\ =\iint _{S}\sin \theta \,d\theta \,d\varphi ,$ ku ${\hat {r}}={\vec {r}}/r$ është vektori njësi që i korrespondon ${\vec {r}}$ , vektori i pozicionit të një zone infinite të vogël të sipërfaqes dS në lidhje me pikën P, dhe ku ${\hat {n}}$ paraqet vektorin normal njësi për dS . Edhe nëse projeksioni në sferën e njësisë në sipërfaqen S nuk është izomorfik, palosjet e shumta konsiderohen saktë sipas orientimit të sipërfaqes të përshkruar nga shenja e prodhimit skalar. ${\hat {r}}\cdot {\hat {n}}$ .

Zbatime praktike

Përcaktimi i intensitetit dhe shkëlqimit të dritës, dhe sasive korresponduese radiometrike, intensitetit të rrezatimit dhe rrezatueshmërisë
Llogaritja e tepricës sferike E të një trekëndëshi sferik
Llogaritja e potencialeve duke përdorur metodën e elementit kufitar (BEM)
Vlerësimi i madhësisë së ligandëve në komplekset metalike, shih këndin e konit të ligandit
Llogaritja e fushës elektrike dhe fuqisë së fushës magnetike rreth shpërndarjes së ngarkesës
Nxjerrja e ligjit të Gausit
Llogaritja e fuqisë emetuese dhe rrezatimit në transferimin e nxehtësisë
Llogaritja e prerjeve tërthore në shpërndarjen Rutherford
Llogaritja e prerjeve tërthore në shpërndarjen Raman
Këndi i ngurtë i konit të pranimit të fibrës optike

Kënde të ngurta ër objektet e zakonshme

Kon, kapak sferik, hemisferë

Këndi i ngurtë i një koni me majën e tij në apeksin e këndit të ngurtë dhe me këndin e apeksit 2 θ, është sipërfaqja e një kapaku sferik në një sferë njësi. $\Omega =2\pi \left(1-\cos \theta \right)\ =4\pi \sin ^{2}{\frac {\theta }{2}}.$ Për θ të vogla të tilla që $\cos(\theta )=1-{\frac {\theta ^{2}}{2}}$ kjo zvogëlohet në $\pi \theta ^{2}$ , sipërfaqja e një rrethi.

Sa më sipër gjendet duke llogaritur integralin e dyfishtë të mëposhtëm duke përdorur elementin njësi të sipërfaqes në koordinata sferike : ${\begin{aligned}\int _{0}^{2\pi }\int _{0}^{\theta }\sin \theta '\,d\theta '\,d\phi &=\int _{0}^{2\pi }d\phi \int _{0}^{\theta }\sin \theta '\,d\theta '\\&=2\pi \int _{0}^{\theta }\sin \theta '\,d\theta '\\&=2\pi \left[-\cos \theta '\right]_{0}^{\theta }\\&=2\pi \left(1-\cos \theta \right).\end{aligned}}$ Kjo formulë mund të nxirret edhe pa përdorimin e analizës matematike . Mbi 2200 vjet më parë Arkimedi vërtetoi se sipërfaqja e një kapaku sferik është gjithmonë e barabartë me sipërfaqen e një rrethi rrezja e të cilit është e barabartë me largësinë nga buzë e kapakut sferik deri në pikën ku boshti i simetrisë së kapakut kryqëzon kapakun. ^[1] Në diagram kjo rreze është dhënë si $2r\sin {\frac {\theta }{2}}.$ Prandaj për një sferë njësi këndi i ngurtë i kapakut sferik është dhënë si $\Omega =4\pi \sin ^{2}{\frac {\theta }{2}}=2\pi \left(1-\cos \theta \right).$ Kur $\theta =\pi /2$ , kapaku sferik bëhet një hemisferë që ka një kënd të ngurtë 2 π .

Këndi i ngurtë i plotësit të konit është $4\pi -\Omega =2\pi \left(1+\cos \theta \right)=4\pi \cos ^{2}{\frac {\theta }{2}}.$ Ky është gjithashtu këndi i ngurtë i pjesës së sferës qiellore që një vëzhgues astronomik i pozicionuar në gjerësinë gjeografike θ mund ta shohë ndërsa Toka rrotullohet. Në ekuator e gjithë sfera qiellore është e dukshme; në secilin pol, vetëm një gjysmë.

Këndi i ngurtë i tendosur nga një segment i një kapaku sferik të prerë nga një plan në këndin γ nga boshti i konit dhe që kalon nëpër majën e konit mund të llogaritet me formulën ^[2] $\Omega =2\left[\arccos \left({\frac {\sin \gamma }{\sin \theta }}\right)-\cos \theta \arccos \left({\frac {\tan \gamma }{\tan \theta }}\right)\right].$ Për shembull, nëse γ = - θ, atëherë formula reduktohet në formulën e kapakut sferik të mësipërm: termi i parë bëhet π, dhe i dyti π cos θ .

^ "Archimedes on Spheres and Cylinders". Math Pages. 2015. {{cite journal}}: Mungon ose është bosh parametri |language= (Ndihmë!)
^ Mazonka. "Solid Angle of Conical Surfaces, Polyhedral Cones, and Intersecting Spherical Caps". arXiv:1205.1396. {{cite arXiv}}: Mungon ose është bosh parametri |language= (Ndihmë!)

[1] "Archimedes on Spheres and Cylinders". Math Pages. 2015. {{cite journal}}: Mungon ose është bosh parametri |language= (Ndihmë!)

[Mazonka-2] Mazonka. "Solid Angle of Conical Surfaces, Polyhedral Cones, and Intersecting Spherical Caps". arXiv:1205.1396. {{cite arXiv}}: Mungon ose është bosh parametri |language= (Ndihmë!)

[1]

[2]