Trajektorja

Ilustrim që tregon trajektoren e drejtimit të një plumbi të shkrepur në një objektiv përpjetë.

Një trajektore ose shteg fluturimi është shtegu që një objekt me masë në lëvizje ndjek nëpër hapësirë në funksion të kohës. Në mekanikën klasike, një trajektore përcaktohet nga mekanika Hamiltoniane nëpërmjet koordinatave kanonike ; kështu, një trajektore e plotë përcaktohet nga vendndodhja dhe njëkohësisht impulsi.

Masa mund të jetë një predhë ose një satelit . Për shembull, mund të jetë një orbitë - rruga e një planeti, asteroidi ose komete ndërsa udhëton rreth një mase qendrore .

Në teorinë e kontrollit, një trajektore është një bashkësi gjendjesh të indeksuara sipas kohës së një sistemi dinamik (shih p.sh. hartën e Puankaresë ). Në matematikën diskrete, një trajektore është një sekuencë $(f^{k}(x))_{k\in \mathbb {N} }$ e vlerave të llogaritura nga zbatimi i përsëritur i një harte $f$ ndaj një elementi $x$ të burimit të saj.

Shembuj

Graviteti i njëtrajtshëm, as zvarritje as erë

Trajektoret e një mase të hedhur në një kënd prej 70°,



    pa zvarritje

    me zvarritje të Stokes
    me zvarritje të Njutonit

Rasti ideal i lëvizjes së një predheje në një fushë gravitacionale uniforme në mungesë të forcave të tjera (si p.sh. tërheqja e ajrit) u hetua për herë të parë nga Galileo Galilei . Neglizhimi i veprimit të atmosferës në formësimin e një trajektoreje do të ishte konsideruar një hipotezë e kotë nga kërkuesit me mendje praktike gjatë gjithë Mesjetës në Evropë . Megjithatë, duke parashikuar ekzistencën e vakumit, që më vonë do të demonstrohej në Tokë nga bashkëpunëtori i tij Evangelista Torricelli, Galileo ishte në gjendje të niste shkencën e ardhshme të mekanikës.. Në një boshllëk të afërt, siç rezulton për shembull në Hënë, trajektorja e tij parabolike e thjeshtuar rezulton në thelb e saktë.

Nxjerrja e ekuacionit të lëvizjes

Supozoni se lëvizja e predhës po matet nga një sistem i rënies së lirë e cila ndodh të jetë në ( x, y ) = (0,0) në t = 0. Ekuacioni i lëvizjes së predhës në këtë kuadër (sipas parimit të njëvlershmërisë ) do të ishte $y=x\tan(\theta )$ . Koordinatat e kësaj kornize të rënies së lirë, në lidhje me sistemin tonë inercial do të ishin $y=-gt^{2}/2$ . Kjo eshte, $y=-g(x/v_{h})^{2}/2$ .

Tani duke përkthyer përsëri në kornizën inerciale, koordinatat e predhës bëhen $y=x\tan(\theta )-g(x/v_{h})^{2}/2$ Kjo eshte:

$y=-{g\sec ^{2}\theta \over 2v_{0}^{2}}x^{2}+x\tan \theta ,$

(ku v ₀ është shpejtësia fillestare, $\theta$ është këndi i ngritjes, dhe g është nxitimi për shkak të gravitetit).

Shtrirja dhe lartësia

Trajektoret e predhave të lëshuara në kënde të ndryshme lartësie, por me të njëjtën shpejtësi prej 10 m/s në një vakum dhe fushë rëndese njëtrajtshme në rënie prej 10 m/s ² . Pikat janë në intervale 0,05 s dhe gjatësia e bishtit të tyre është në proporcion linear me shpejtësinë e tyre. t = koha nga nisja, T = koha e fluturimit, R = diapazoni dhe H = pika më e lartë e trajektores (treguar me shigjeta).

Diapazoni, R, është largësia më e madhe që objekti përshkon përgjatë boshtit x në sektorin I. Shpejtësia fillestare, v _i, është shpejtësia me të cilën objekti në fjalë lëshohet nga pika e origjinës. Këndi fillestar, θ _i, është këndi në të cilin objekti në fjalë lëshohet. G është tërheqja përkatëse gravitacionale e objektit brenda një mjedisi null.

$R={v_{i}^{2}\sin 2\theta _{i} \over g}$

Lartësia, h, është lartësia më e madhe parabolike që objekti arrin brenda trajektores së tij

$h={v_{i}^{2}\sin ^{2}\theta _{i} \over 2g}$

Këndi i lartësisë

Një shembull që tregon se si të llogaritet trajektorja e plumbave

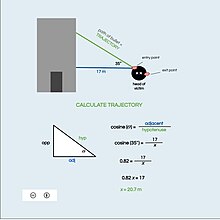
Për sa i përket këndit të ngritjes $\theta$ dhe shpejtësinë fillestare $v$ :

$v_{h}=v\cos \theta ,\quad v_{v}=v\sin \theta \;$

duke i dhënë diapazonit si

$R=2v^{2}\cos(\theta )\sin(\theta )/g=v^{2}\sin(2\theta )/g\,.$

Ky ekuacion mund të riorganizohet për të gjetur këndin për një diapazon të kërkuar

$\theta ={\frac {1}{2}}\sin ^{-1}\left({\frac {gR}{v^{2}}}\right)$ (Ekuacioni II: këndi i lëshimit të predhës)

Vini re se funksioni sinus është i tillë që ka dy zgjidhje për $\theta$ për një shtrirje të caktuar $d_{h}$ . Këndi $\theta$ dhënia e shtrirjes maksimale mund të gjendet duke marrë parasysh derivatin ose $R$ në lidhje me $\theta$ dhe duke e vendosur atë në zero.

${\mathrm {d} R \over \mathrm {d} \theta }={2v^{2} \over g}\cos(2\theta )=0$

e cila ka një zgjidhje jo triviale në $2\theta =\pi /2=90^{\circ }$, ose $\theta =45^{\circ }$ . Diapazoni maksimal është atëherë $R_{\max }=v^{2}/g\,$ . Në këtë kënd $\sin(\pi /2)=1$, pra lartësia maksimale e fituar është ${v^{2} \over 4g}$ .

Për të gjetur këndin që jep lartësinë maksimale për një shpejtësi të caktuar llogaritni derivatin e lartësisë maksimale $H=v^{2}\sin ^{2}(\theta )/(2g)$ në lidhje me $\theta$, kjo eshte ${\mathrm {d} H \over \mathrm {d} \theta }=v^{2}2\cos(\theta )\sin(\theta )/(2g)$ e cila është zero kur $\theta =\pi /2=90^{\circ }$ . Pra, lartësia maksimale $H_{\mathrm {max} }={v^{2} \over 2g}$ fitohet kur predha qëllohet drejt lart.