Konvolucioni

Krahasimi pamor i thurjes, ndër-korrelacionit dhe autokorrelacionit . Për operacionet që përfshijnë funksionin f, dhe duke supozuar se lartësia e f është 1.0, vlera e rezultatit në 5 pika të ndryshme tregohet nga zona e hijezuar poshtë secilës pikë. Simetria e f është arsyeja $f\star g$ dhe $g*f$ janë identike në këtë shembull.

Në matematikë (në veçanti, analiza funksionale ), konvolucioni ose shqip thurja është një veprim matematikor mbi dy funksione ( $f$ dhe $g$ ) që jep një funksion të tretë ( $f*g$ ) që shpreh se si forma e njërës modifikohet nga tjetra. Termi konvolucion i referohet si funksionit rezultant ashtu edhe procesit të llogaritjes së tij. Përkufizohet si integrali i prodhimit të dy funksioneve pasi njëri është reflektuar rreth boshtit y dhe është zhvendosur. Zgjedhja se cili funksion reflektohet dhe zhvendoset përpara integralit nuk e ndryshon rezultatin e integralit (shih ndërrueshmëria ). Integrali vlerësohet për të gjitha vlerat e zhvendosjes, duke prodhuar funksionin e konvolucionit (thurjes).

Disa tipare të thurjes janë të ngjashme me korrelacionin kryq : për funksionet me vlera reale, të një ndryshoreje të vazhdueshme ose diskrete, thurja ( $f*g$ ) ndryshon nga korrelacioni kryq ( $f\star g$ ) vetëm se ose $f(x)$ ose $g(x)$ pasqyrohet rreth boshtit y në thurje; pra është një ndërlidhje e $g(-x)$ dhe $f(x)$, ose $f(-x)$ dhe $g(x)$.  Për funksionet me vlerë komplekse, operatori i ndërlidhjes është i konjuguari hermitian i veprimit të konvolucionit.

Thurja ka aplikime që përfshijnë probabilitetin, statistikën, akustikën, spektroskopinë, përpunimin e sinjalit dhe përpunimin e imazhit, gjeofizikën, inxhinierinë, fizikën, vizionin kompjuterik dhe ekuacionet diferenciale .

Thurja mund të përcaktohet për funksionet në hapësirën Euklidiane dhe grupe të tjera (si struktura algjebrike ). Për shembull, funksionet periodike, të tilla si transformimi Furie në kohë diskrete, mund të përcaktohen në një rreth nga thurja rrethore. Një thurje diskrete mund të përcaktohet për funksionet në grupin e numrave të plotë .

Përgjithësimet e konvolucionit kanë aplikime në fushën e analizës numerike dhe algjebrës lineare numerike, dhe në projektimin dhe zbatimin e filtrave të përgjigjes së impulsit të fundëm në përpunimin e sinjalit.

Llogaritja e inversit të operacionit të konvolucionit njihet si dekonvolucion ose shthurje .

Përkufizimi

Konvolucioni i $f$ dhe $g$ shkruhet f∗g, duke treguar veprimin me simbolin ∗ . Përkufizohet si integrali i prodhimit të dy funksioneve pasi njëri është reflektuar rreth boshtit y dhe është zhvendosur. Si i tillë, është një lloj i veçantë transformimi integral :

$(f*g)(t):=\int _{-\infty }^{\infty }f(\tau )g(t-\tau )\,d\tau .$

Një përkufizim i njëvlershëm është (shih komutativitetin ):

$(f*g)(t):=\int _{-\infty }^{\infty }f(t-\tau )g(\tau )\,d\tau .$

Megjithëse përdoret simboli $t$ më lart, ai nuk ka nevojë të përfaqësojë rrafshin e kohës. Në çdo $t$, formula e konvolucionit mund të përshkruhet si zona nën funksionin $f(\tau )$ e peshuar nga funksioni $g(-\tau )$ i zhvendosur me madhësinë $t$ . Ndërsa $t$ ndryshon, funksioni i peshimit $g(t-\tau )$ thekson pjesë të ndryshme të funksionit hyrës $f(\tau )$; Nëse $t$ është një vlerë pozitive, atëherë $g(t-\tau )$ është e barabartë me $g(-\tau )$ që rrëshqet ose zhvendoset përgjatë boshtit $\tau$ në të djathtë (drejt +∞ ) me madhësinë $t$, ndërsa nëse t është një vlerë negative, atëherë $g(t-\tau )$ është e barabartë me $g(-\tau )$ që rrëshqet ose zhvendoset në të majtë (drejt -∞ ) me madhësinë $|t|$ .

Marrëdhëniet me transformimet e tjera

Jepen dy funksione $f(t)$ dhe $g(t)$ me transformime të dyanshme të Laplasit (transformimi i Laplasit me dy anë)

$F(s)=\int _{-\infty }^{\infty }e^{-su}\ f(u)\ {\text{d}}u$

dhe

$G(s)=\int _{-\infty }^{\infty }e^{-sv}\ g(v)\ {\text{d}}v$

veprimi i thurjes $(f*g)(t)$ mund të përkufizohet si transformimi i anasjelltë i Laplasit i prodhimit të $F(s)$ dhe $G(s)$ . Më saktë,

${\begin{aligned}F(s)\cdot G(s)&=\int _{-\infty }^{\infty }e^{-su}\ f(u)\ {\text{d}}u\cdot \int _{-\infty }^{\infty }e^{-sv}\ g(v)\ {\text{d}}v\\&=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }e^{-s(u+v)}\ f(u)\ g(v)\ {\text{d}}u\ {\text{d}}v\end{aligned}}$

Le të jetë $t=u+v$ sikurse

${\begin{aligned}F(s)\cdot G(s)&=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }e^{-st}\ f(u)\ g(t-u)\ {\text{d}}u\ {\text{d}}t\\&=\int _{-\infty }^{\infty }e^{-st}\underbrace {\int _{-\infty }^{\infty }f(u)\ g(t-u)\ {\text{d}}u} _{(f*g)(t)}\ {\text{d}}t\\&=\int _{-\infty }^{\infty }e^{-st}(f*g)(t)\ {\text{d}}t\end{aligned}}$

Vini re se $F(s)\cdot G(s)$ është transformimi i dyanshëm i Laplasit për $(f*g)(t)$ . Një derivim i ngjashëm mund të bëhet duke përdorur transformimin e njëanshëm të Laplasit.

Veprimi i konvolucionit përshkruan gjithashtu daljen (në termat e hyrjes) të një klase të rëndësishme veprimesh të njohura si lineare dhe të pandryshueshme në kohë (LTI). Shih teorinë e sistemit LTI për një derivim të thurjes si rezultat i kufizimeve LTI. Përsa i përket transformimeve Furie të hyrjes dhe daljes së një veprimi LTI, nuk krijohen përbërës të rinj të frekuencës. Ato ekzistuese vetëm sa janë modifikuar (amplitudë dhe/ose fazë). Me fjalë të tjera, transformimi i daljes është prodhimi pikësor i transformimit të hyrjes me një transformim të tretë (i njohur si funksioni i transferimit ).

Shpjegimi pamor

Shprehni çdo funksion në terma të një ndryshoreje lolo $\tau$, Reflektoni një nga funksionet $g(\tau )\longrightarrow g(-\tau )$ Shtoni një shmangie fillestare $t$ e cila e lejon $g(-\tau )$ të rrëshqasë përgjatë boshtit $\tau$. Nëse $t$ është një vlerë pozitive atëherë $g(t-\tau )$ është e barabartë me $g(-\tau )$ që rrëshqet ose zhvendoset përgjatë boshtit $\tau$ drejt të djathtës me madhësinë $t$. Nëse $t$ është një vlerë negative atëherë $g(t-\tau )$ është e barabartë me $g(-\tau )$ që rrëshqet ose zhvendoset përgjatë boshtit $\tau$ drejt të majtës me madhësinë $t$. Filloni $t$ nga $-\infty$ dhe rrëshqiteni deri në $+\infty$. Kudoqoftë që funksionet priten, gjeni integralin e prodhimit të tyre. Me fjalë të tjera, në kohën $t$ llogarisni sipërfaqen nën funksionin $f(\tau )$ i peshuar nga funksioni $g(t-\tau )$ Stampa:Ordered list Forma e valës që rezulton (nuk tregohet këtu) është konvolucioni i funksioneve $f$ dhe $g$ . Nëse $f(t)$ është një impuls njësi, rezultati i këtij procesi është thjesht $g(t)$ . Formalisht: $\int _{-\infty }^{\infty }\delta (\tau )g(t-\tau )\,d\tau =g(t)$
Në këtë shembull, "pulsi" me ngjyrë të kuqe, $\ g(\tau ),$ është një funksion çift $(\ g(-\tau )=g(\tau )\ ),$ kështu që thurja është e barabartë me korrelacionin. Një fotografi e këtij "filmi" tregon funksionet $g(t-\tau )$ dhe $f(\tau )$ (me blu) për disa vlera të parametrit $t,$ e cila është përcaktuar në mënyrë arbitrare si largësia përgjatë boshtit $\tau$ nga pika $\tau =0$ në qendër të pulsit të kuq. Sasia e të verdhës është sipërfaqja e produktit $f(\tau )\cdot g(t-\tau ),$ llogaritur nga integrali i konvolucionit/korrelacionit. Filmi është krijuar duke ndryshuar vazhdimisht $t$ dhe rillogaritur integralin. Rezultati (i treguar me të zezë) është një funksion i $t,$ por vizatohet në të njëjtin bosht si $\tau ,$ për lehtësi dhe krahasim.	</img>
Në këtë përshkrim, $f(\tau )$ mund të përfaqësojë përgjigjen e një qarku RC ndaj një pulsi të ngushtë që ndodh në $\tau =0.$ Me fjalë të tjera, nëse $g(\tau )=\delta (\tau ),$ rezultati i konvolucionit është thjesht $f(t).$ Por kur $g(\tau )$ është puls më i gjerë (në të kuqe), përgjigja është një version "poroz" i $f(t).$ Ajo fillon në $t=-0.5,$ sepse kemi përcaktuar $t$ si largësinë nga $\tau =0$ në qendër të pulsit të gjerë (në vend të skajit kryesor).	</img>

Thurja diskrete

Animacion diskret 2D i thurjes

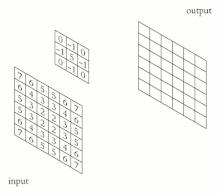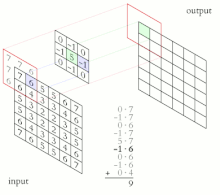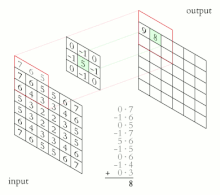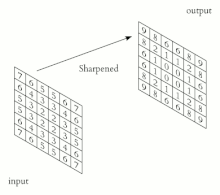
Për funksionet me vlera komplekse $f$, $g$ të përcaktuar në bashkësinë $\mathbb {Z}$ të numrave të plotë, konvolucioni diskret i $f$ dhe $g$ jepet nga:

$(f*g)[n]=\sum _{m=-\infty }^{\infty }f[m]g[n-m],$

ose në mënyrë të njëvlershme (shih ndërrimin ) nga:

$(f*g)[n]=\sum _{m=-\infty }^{\infty }f[n-m]g[m].$

Funksionet e integrueshëm

Konvolucioni i $f$ dhe $g$ ekziston nëse $f$ dhe $g$ janë të dy funksione të integrueshme sipas Lebegut në $L^{1}$ ( $R^{d}$), dhe në këtë rast $f\star g$ është gjithashtu i integrueshëm (Stein & Weiss 1971) . Kjo është pasojë e teoremës Toneli . Kjo është gjithashtu e vërtetë për funksionet në $L^{1}$ nën konvolucionin diskret, ose më në përgjithësi për konvolucionin në çdo grup .

Po kështu, nëse $f\in L^{1}({\boldsymbol {R}}^{d})$ dhe $f\in L^{1}({\boldsymbol {R}}^{d})$ ku $1\leq p\leq \infty$ , pastaj $f\star g\in L^{1}({\boldsymbol {R}}^{d})$ , dhe

$\|{f}*g\|_{p}\leq \|f\|_{1}\|g\|_{p}.$

Në rastin e veçantë p = 1, kjo tregon se $L^{1}$ është një algjebër Banah nën konvolucionin (dhe barazia e të dy anëve vlen nëse $f$ dhe $g$ janë jonegative pothuajse kudo).

Në përgjithësi, mosbarazimi i Young nënkupton që thurja është një hartë bilineare e vazhdueshme midis hapësirave të përshtatshme $L^{p}$ . Në mënyrë të veçantë, nëse 1 ≤ p, q, r ≤ ∞ kënaq:

${\frac {1}{p}}+{\frac {1}{q}}={\frac {1}{r}}+1,$

pastaj

$\left\Vert f*g\right\Vert _{r}\leq \left\Vert f\right\Vert _{p}\left\Vert g\right\Vert _{q},\quad f\in {\mathcal {L}}^{p},\ g\in {\mathcal {L}}^{q},$

i tillë që konvolucioni është një hartë bilineare e vazhdueshme nga $L^{p}\times L^{q}$ në $L^{r}$ . Mosbarazimi Jang për thurjen është gjithashtu i vërtetë në kontekste të tjera (grupi rrethor, konvolucioni në $\mathbb {Z}$ ). Mosbarazimi e mëparshme nuk është stikt në vijën reale: kur 1 < p, q, r < ∞, ekziston një konstante $B_{p,q}$< 1 e tillë që:

$\left\Vert f*g\right\Vert _{r}\leq B_{p,q}\left\Vert f\right\Vert _{p}\left\Vert g\right\Vert _{q},\quad f\in {\mathcal {L}}^{p},\ g\in {\mathcal {L}}^{q}.$

Vlera optimale e $B_{p,q}$ u zbulua në 1975 dhe në mënyrë të pavarur në 1976, shih mosbarazimin Brascamp–Lieb .

Një vlerësim më i fortë është i vërtetë me kusht që 1 < p, q, r <∞ :

$\|f*g\|_{r}\leq C_{p,q}\|f\|_{p}\|g\|_{q,w}$

ku $\|g\|_{q,w}$ është norma e dobët $L^{q}$ . Convolution gjithashtu përcakton një hartë bilineare të vazhdueshme $L^{p,w}\times L^{q,w}\to L^{r,w}$ për $1<p,q,r<\infty$, për shkak të mosbarazimiz së dobët të Jangut:

$\|f*g\|_{r,w}\leq C_{p,q}\|f\|_{p,w}\|g\|_{r,w}.$

Vetitë

Vetitë algjebrike

Vetia e ndërrimit

$f\star g=g\star f$

Provë: Nga përkufizimi

$(f*g)(t)=\int _{-\infty }^{\infty }f(\tau )g(t-\tau )\,d\tau$

Ndryshimi i ndryshores së integrimit në $u=t-\tau$ jep si më sipër

Vetia e shoqërimit

$(f\star g)\star h=f\star (g\star h)$

$$f*(g*h)=(f*g)*h$$

Vetia e shpërndarjes

$f\star (g+h)=f\star g+f\star h$

$$f*(g+h)=(f*g)+(f*h)$$

Shoqërimi me shumëzimin skalar

$a(f\star g)=(af)\star g$

$$a(f*g)=(af)*g$$

Identiteti shumëfishues

Asnjë algjebër funksionesh nuk ka një identitet për konvolucionin. Mungesa e identitetit zakonisht nuk është një shqetësim i madh, pasi shumica e koleksioneve të funksioneve në të cilat kryhet konvolucioni mund të thuren me një shpërndarje delta (një impuls njësi, i përqendruar në zero) ose, të paktën (siç është rasti i L ¹ ) pranon përafrimet me identitetin . Hapësira lineare e shpërndarjeve të mbështetura në mënyrë kompakte, megjithatë, pranon një identitet nën thurje.

$f\star \delta =f$

Konkretisht,

$$f*\delta =f$$

Elementi i anasjelltë

Disa shpërndarje S kanë një element të anasjelltë S ⁻¹ për thurjen që më pas duhet të kënaqë

$S^{-}1\star S=\delta$

$$S^{-1}*S=\delta$$

Konjugimi kompleks

$${\overline {f*g}}={\overline {f}}*{\overline {g}}$$

Marrëdhënia me diferencimin

$$(f*g)'=f'*g=f*g'$$

${\begin{aligned}(f*g)'&={\frac {d}{dt}}\int _{-\infty }^{\infty }f(\tau )g(t-\tau )\,d\tau \\&=\int _{-\infty }^{\infty }f(\tau ){\frac {\partial }{\partial t}}g(t-\tau )\,d\tau \\&=\int _{-\infty }^{\infty }f(\tau )g'(t-\tau )\,d\tau =f*g'.\end{aligned}}$

Marrëdhënia me integrimin

Nëse ${\textstyle F(t)=\int _{-\infty }^{t}f(\tau )d\tau ,}$ dhe ${\textstyle G(t)=\int _{-\infty }^{t}g(\tau )\,d\tau ,}$ pastaj

$$(F*g)(t)=(f*G)(t)=\int _{-\infty }^{t}(f*g)(\tau )\,d\tau .$$

Teorema e konvolucionit

Teorema e konvolucionit thotë se

${\mathcal {F}}\{f*g\}={\mathcal {F}}\{f\}\cdot {\mathcal {F}}\{g\}$

ku ${\mathcal {F}}\{f\}$ tregon transformimin Furier të $f$ .

Konvolucioni në llojet e tjera të transformimeve

Versionet e kësaj teoreme vlejnë edhe për transformimin e Laplasit, transformimin e Laplasit me dy anë, transformimin Z dhe transformimin e Mellinit .

Aplikacionet

Turbullimi Gausian mund të përdoret për të marrë një imazh dixhital të lëmuar në shkallë gri të një printimi gjysmëton .

Konvolucioni dhe veprimet e lidhura me të gjenden në shumë zbatime në shkencë, inxhinieri dhe matematikë.

• Rrjetet nervore konvolucionale zbatojnë shumë bërthama thurje në kaskadë me aplikime në vizionin e makinës dhe inteligjencën artificiale . Megjithëse këto janë në të vërtetë korrelacione të kryqëzuara dhe jo thurje në shumicën e rasteve.
• Në përpunimin e imazheve jo të bazuar në rrjete nervore
  • Në përpunimin dixhital të imazhit, filtrimi thuror luan një rol të rëndësishëm në shumë algoritme të rëndësishme në zbulimin e skajeve dhe proceset përkatëse (shih Kernel (përpunimi i imazhit) )
  • Në optikë, një fotografi jashtë fokusit është një thurje e imazhit të mprehtë me një funksion lente. Termi fotografik për këtë është bokeh .
  • Në aplikacionet e përpunimit të imazhit si shtimi i turbullimit.
• Në përpunimin dixhital të të dhënave
  • Në kiminë analitike, filtrat zbutës Savitzky-Golay përdoren për analizën e të dhënave spektroskopike.
  • Në statistikë, një mesatare lëvizëse e peshuar është një thurje.
• Në akustikë, reverberimi është ndërthurja e tingullit origjinal me jehona nga objektet që rrethojnë burimin e zërit.
  • Në përpunimin e sinjalit dixhital, konvolucioni përdoret për të hartuar përgjigjen e impulsit të një dhome reale në një sinjal audio dixhital.
  • Në muzikën elektronike konvolucioni është imponimi i një strukture spektrale ose ritmike mbi një tingull.
• Në inxhinierinë elektrike, konvolucioni i një funksioni ( sinjali i hyrjes ) me një funksion të dytë (përgjigja e impulsit) jep daljen e një sistemi linear të pandryshueshëm në kohë (LTI). Në çdo moment, dalja është një efekt i mbledhur i të gjitha vlerave të mëparshme të funksionit të hyrjes, me vlerat më të fundit që zakonisht kanë ndikimin më të madh (të shprehur si një faktor shumëzues). Funksioni i përgjigjes së impulsit siguron atë faktor në funksion të kohës së kaluar që kur ka ndodhur çdo vlerë hyrëse.
• Në fizikë, kudo që ka një sistem linear me një " parim mbivendosje ", një operacion konvolucioni shfaqet. Për shembull, në spektroskopinë zgjerimi i linjës për shkak të efektit Doppler më vete jep një formë të vijës spektrale Gaussian dhe vetëm zgjerimi i përplasjes jep një formë të linjës Lorencian . Kur të dy efektet janë operative, forma e linjës është një ndërthurje e Gaussian-it dhe Lorencian-it, një funksion Voigt .
  • Në spektroskopinë e fluoreshencës të zgjidhur me kohë, sinjali i ngacmimit mund të trajtohet si një zinxhir pulsesh delta, dhe fluoreshenca e matur është një shumë e zbërthimeve eksponenciale nga çdo puls delta.
  • Në dinamikën e lëngjeve llogaritëse, modeli i turbulencës së simulimit të vorbullave të mëdha (LES) përdor operacionin e konvolucionit për të ulur gamën e shkallëve të gjatësisë të nevojshme në llogaritje duke reduktuar kështu koston llogaritëse.
• Në teorinë e probabilitetit, shpërndarja e probabilitetit të shumës së dy ndryshoreve të rastit të pavarura është konvolucioni i shpërndarjeve të tyre individuale.
• Në sistemet e planifikimit të trajtimit me radioterapi, pjesa më e madhe e të gjitha kodeve moderne të llogaritjes zbaton një algoritëm thurje-mbivendosje . 
• Në besueshmërinë strukturore, indeksi i besueshmërisë mund të përcaktohet bazuar në teoremën e konvolucionit.
  • Përkufizimi i indeksit të besueshmërisë për funksionet e gjendjes kufitare me shpërndarje jonormale mund të përcaktohet në përputhje me funksionin e përbashkët të shpërndarjes . Në fakt, funksioni i shpërndarjes së përbashkët mund të merret duke përdorur teorinë e konvolucionit.
• Në llogaritjen thyesore konvolucioni është i rëndësishëm në përkufizime të ndryshme të derivatit integral dhe thyesor.